Review

Problem 1:

Two 1 m² conducting plates are separated by a distance x = 1 mm and carry charge ±Q = 10^-3 C, respectively.  Find the external force needed to keep the plates of this capacitor 1 mm apart using energy considerations.

Solution:

• Concepts:
  The electric field inside a capacitor, electrostatic energy
• Reasoning:
  Approximation:  E = σ/ε₀  between the plates,  E = 0 outside.
• Details of the calculation:
  Let the negative plate lie in the x = 0 plate and the positive plate in the x = 1 mm plane.
  The electrostatic force on the positive plate is F = -dU/dx.  U = (ε₀/2) ∫_{all space}E²dV = (ε₀/2)E²Ax.
  dU/dx = (ε₀/2)E²A = Q²/(2Aε₀)
  F_ext = dU/dx = 5.65*10⁴ N.

Problem 2:

Assume a photon gas is described by the Planck distribution

n(ν,T) = (8π/c³)[ν²/(exp(hν/(kT)) - 1)],

where ν is the photon frequency and T is the temperature of the gas.
(a)  Find the energy density u(T) of the photon gas.
(b)  The intensity per unit frequency interval of the radiation emitted by the blackbody is
I(ν,T) = ¼u(ν,T) c. 
Find an expression for the Stefan-Boltzmann constant σ.

You may find this definite integral useful.
∫₀^∞xⁿ dx/(e^x - 1) = n! ζ(n+1), where ζ(n) is the Riemann zeta function.
 ζ(1) = ∞,   ζ(2) = π²/6,    ζ(3) ≈ 1.202,    ζ(4) = π⁴/90,   ζ(5) ≈ 1.037. 

Solution:

• Concepts:
  Radiation laws
• Reasoning:
  The Stefan-Boltzmann Law gives the total energy emitted at all wavelengths by a black body.
• Details of the calculation:
  (a)  The number of photons per unit frequency interval is n(ν,T).
  The energy density per unit frequency interval is
  u(ν,T) = hν*n(ν,T) = (8πν²/c³)hν/(exp(hν/(kT)) - 1).
  
  To find the total energy density, integrate over all frequencies.
  u(T) = ∫₀^∞(8π/c³)hν³ dν/(exp(hν/(kT)) - 1) = (8πk⁴T⁴/(h³c³))∫₀^∞ x³ dx/(exp(x) - 1)
  = (8πk⁴T⁴/(h³c³)) π⁴/15 = 8π⁵k⁴T⁴/(15h³c³) = aT⁴.
  a = 8π⁵k⁴/(15h³c³).
  u(T) is proportional to T⁴.
  
  (b)  I(T) = ¼u(T)c =  2π⁵k⁴T⁴/(15h³c²) = σT⁴.
  σ = 2π⁵k⁴/(15h³c²) ≈ 5.67*10^-8 Wm^-2K^-4.

Problem 3:

A boat with mass m₀, experiencing a drag force f_drag = -bv, is moving with constant velocity v₀ because the motor is set to exactly cancel the drag force.  At t = 0 it starts to rain straight down, and water accumulates inside the boat.  The mass of the boat increases at a constant rate λ = dm/dt.  
(a)  If the force the motor exerts stays constant, find the acceleration of the boat.
(b)  Find the boat's velocity as a function of time.

Solution:

• Concepts:
  Newton's 2^nd law:  F = dp/dt, dp = mdv + vdm
• Reasoning:
  This is a one-dimensional problem.  The sign of the vector quantities is the direction indicator.
  The system consists of the rainwater, with zero momentum and the boat with momentum p.  In a time interval dt a small amount dm of the water receives an impulse vdm.  In the same time interval the velocity of the boat changes by dv.  The total momentum change of the system is
  dp = mdv + vdm = -b(v - v₀)dt.
• Details of the calculation:
  (a)  p = mv,  dp/dt = mdv/dt + vdm/dt = -b(v - v₀) .
  dv/dt + vλ/(m₀ + λt) = -b(v - v₀)/(m₀ + λt).
  dv/dt = -v(λ + b)/(m₀ + λt) +  bv₀/(m₀ + λt).
  
  (b)  Let t' = m₀ + λt.  Then dv/dt' + v(1 + b/λ)/t' = (bv₀/λ)/t'.
  To a particular solution of the first-order inhomogeneous differential equation we add the solution of the homogeneous differential equation to find the most general solution.
  An inhomogeneous solution:  dv/dt' = 0 -->  v = bv₀/(λ + b)
  Homogeneous solution:  dv/dt' = -v(1 + b/λ)/t',  v(t') = At'^{(-1 - b/λ)}
  Most general solution:
  v(t) = bv₀/(λ + b) + A(m₀ + λt)^{(-1 - b/λ)}.
  The initial condition, v(0) = v₀ determines the constant A.

Problem 4:

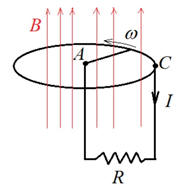Refer to the figure.  One end of a conducting rod rotates with angular velocity ω in a circle of radius a making contact with a horizontal, conducting ring of the same radius.  The other end of the rod is fixed.  Stationary conducting wires connect the fixed end of the rod (A) and a fixed point on the ring (C) to either end of a resistance R.  A uniform vertical magnetic field B passes through the ring.

(a)  Find the current I flowing through the resistor and the rate at which heat is generated in the resistor.
(b)  What is the sign of the current, if positive I corresponds to flow in the direction of the arrow in the figure?
(c)  What torque must be applied to the rod to maintain its rotation at the constant angular rate ω? 
What is the rate at which mechanical work must be done?

Solution:

• Concepts:
  Motional emf
• Reasoning:
  The conducting rod is moving in a plane perpendicular to B.
• Details of the calculation:
  (a)  Speed of the rod as a function of the distance r from the origin: v(r) = ωr.
  Force on an electron: F_e = q_evB = q_eBωr.  (towards point A)
  Work done per unit charge: emf = Bω∫₀^ardr = Bωa²/2.
  Assume that the resistance of the conducting rod and the wires is negligible.
  I = emf/R = Bωa²/(2R) is the current flowing through the resistor.
  P_e = I²R = B²ω²a⁴/(4R) is the rate heat is generated.
  (b)  The sign of the current is positive.
  (c)  Force on a section dr of the current carrying rod:  dF = IdrB  (direction clockwise in the figure).
  An external force of equal magnitude and opposite direction is needed to maintain the constant angular speed.
  dτ = rdF = r IBdr,  τ = IB∫₀^ardr = IBa²/2 = B²ωa⁴/(4R).
  The rate at which mechanical work is done is P_m = τω =  B²ω²a⁴/(4R) = P_e.

Problem 5:

²³⁸Pu decays by α-emission with a half-life of 87 years.
²³⁸Pu --> ²³⁴U + α.
The half-life of ²³⁴U is much longer, 3.5*10⁵ years (ignore this decay).
The heat produced in this decay can be converted into useful electricity by radio-thermal generators (RTG's).  The Voyager 2 space probe, which was launched in August 1977, flew past four planets, including Saturn, which it reached in August 1981.
How much plutonium would an RTG on Voyager 2 with 5.5 % efficiency have to carry at the start to deliver at least 395 W of electric power when the probe flies past Saturn?

Masses:
⁴He:  4.002603 u,
²³⁴U: 234.040947 u
²³⁸Pu:  238.049555 u
Conversion:  1 u = 931.5 MeV

Solution:

• Concepts:
  Nuclear decay
• Reasoning:
  N = N₀exp(-λt),  R = R₀exp(-λt),  R₀ = λN₀.  R = decay rate.
  λ = ln2/t_½ = 7.97*10^-3/year.
• Details of the calculation:
  Each decay releases E = (238.049555 - 234.040947 - 4.002603) * 931.5 MeV  = 8.96*10^-13 J of energy.
  To release 395 W with 5.5% efficiency we need  a decay rate of
  395/(0.055 * 8.96*10^-13)/s = 8.01*10¹⁵/s = 2.53*10²³/year.
  R(t = 4 y) = 2.53*10²³/year = R₀exp(-7.97*10^-3*4).
  R₀ = 2.61*10²³/year.  N₀ = R₀/λ = 3.27*10²⁵.
  We need N₀/N_A = 54.4 mole of plutonium or 12.9 kg of plutonium at the beginning of the mission.