More Problems

Problem 1:

A puck of mass 80 g and radius 4 cm slides along an air table at a speed of 1.5 m/s.  It makes a glancing collision with a second puck of radius 6 cm and mass 120 g (initially at rest) such that their rims just touch.  The pucks stick together and spin after the collision.
(a) What is the angular momentum of the system relative to the center of mass?
(b) What is the angular velocity about the center of mass after the collision? 

Solution:

• Concepts:
  Momentum and angular momentum conservation
• Reasoning:
  The system consists of the two pucks.  No external forces and torques act on the system, so the total momentum and angular momentum of the system are conserved.
• Details of the calculation:
  Let the center of the 120 g mass be at the origin before the collision.
  (a)  Before the collision, the y-coordinate of the CM is
  (m₁y₁ + m₂y₂)/M = (0.08*0.1/0.2) m = 0.04 m.
  The x-coordinate of the CM is (m₁x₁ + m₂x₂)/M = (0.08/0.2)x₁ = (0.4)x₁.
  The velocity of the CM is
  v_CM = dx_CM/dt = (0.4) dx₁/dt  = (0.4)1.5 m/s = 0.6 m/s in the x-direction.
  In the lab frame the m₁ moves with velocity v = 1.5 m/s i 
  and the CM moves with v_CM = 0.6 m/s i.
  With respect to the CM m₁ moves with velocity v₁ = v - v_CM =  0.9 i m/s ,
  and m₂ moves with velocity v₂ = 0 - v_CM =  -0.6 i m/s.
  The angular momentum of the system about the CM is
  L = -(m₁v₁(y₁ - y_CM) + m₂v₂y_CM ) k = -(7.2*10^-3 kg m²/s) k.
  
  (b)  In the collision momentum and angular momentum are conserved.
  The total angular momentum about the CM after the collision is Iω = -(7.2*10^-3 kg m²/s )k.
  The moment of inertia of the system about the CM is I = I₁ +  I₂, where I₁ = I_CM1 + M₁R₁², and I₂ = I_CM2 + M₂R₂².
  I₁ = (1/2) 0.08 kg(0.04 m)² + 0.08 kg(0.06 m)² = 3.52*10^-4 kg m².
  I₂ = (1/2) 0.12 kg(0.06 m)² + 0.12 kg(0.04 m)² = 4.08*10^-4 kg m².
  I = I₁ + I₂ = 7.6*10^-4kg m².
  ω = L/I = -(9.47/s) k.
  To find the moment of inertia of the composite object after the collision the parallel axis theorem was used.

Problem 2:

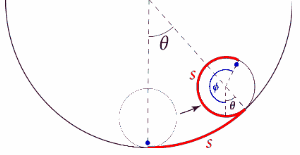
A hoop of radius r can roll inside a fixed circular track of radius R, as shown in the figure.  If the hoop starts at θ = 90^o from rest, what is its angular speed dφ/dt at θ = 45^o?

Solution:

• Concepts:
  Energy conservation
• Reasoning:
  Rolling involves only static friction and gravity is a conservative force.
• Details of the calculation:
  The angles θ and φ are connected through the equation of constraint Rθ = rφ + rθ.
  (R - r)θ = rφ.
  E = T + U = 0.  We set the zero of the potential energy at θ = 90^o.
  ½m(R - r)²(dθ/dt)² + ½mr²(dφ/dt)² - mg(R - r)cosθ = 0.
  (dθ/dt)² = gcosθ/(R - r).
  (dφ/dt)² = g(R - r)cosθ/r² = g(R - r)/(√2r²).
  The angular velocity of the hoop at θ = 45^o is dφ/dt = (g(R - r)/(√2r²))^½.

Problem 3:

(a)  Show that the angular deviation ε of a plumb line (a simple pendulum at rest) from the true vertical at a point on the earth's surface at a northern latitude λ is
ε = (R Ω² sinλ cosλ)/(g - R Ω² cos²λ).
(R = radius of the earth = 6.36*10⁶ m.  Ω = angular speed = 7.3*10^-5/s.  At λ = 45^o, ε = 1.73*10^-3 rad ~ 0.1 deg.)

(b)  An object is dropped from a height h above the earth's surface at latitude λ.  Find the magnitude and direction of its deflection from the plumb line position when it hits the ground in terms of h and g_eff.  Here g_eff is the acceleration due to gravity already corrected for the centrifugal force, g_eff = g + O(Ω²).  Neglect terms of order Ω² and air resistance, and consider only small vertical heights.

Solution:

• Concepts:
  Motion in an accelerating frame
• Reasoning:
  
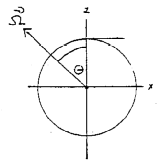
  Assume an observer in the rotating frame at mid latitudes λ = 90^o - θ.
  The equations of motion in a rotating coordinate system contain fictitious forces.
  mdv/dt = F_inertial - mΩ × (Ω × r) - 2mΩ × v.
• Details of the calculation:
  The pendulum bob is at rest.  The net force on the bob is zero.
  F_inertial - mΩ × (Ω × r) = 0.
  F_inertial = -mg k + T. (T is the tension.)
  Ω × r = ΩRsinθ j.
  Ω × (Ω × r) = ΩRsinθ (Ω × j) = ΩRsinθ (Ω_x k - Ω_z i)
  = -ΩRsinθ (Ω sinθ k + Ω cosθ i).
  
  -mg k + mΩ²R sin²θ k + T_z k  - mΩ²Rsinθ cosθ i + T_x i = 0.
  T_z = mg - mΩ²R sin²θ,  T_x = -mΩ²Rsinθcosθ.
  tan(ε) = ε = -T_x/T_z = (Ω²Rsinθcosθ)/(g - Ω²R sin²θ).
  ε = (R ω² sinλ cosλ)/(g - R ω² cos²λ).
  
  (b)  mdv/dt = mg_eff - 2mΩ × v.
  dv_z/dt = -g_eff ,  dv_y/dt = 2Ω_xv_z.
  (Ω × v_y j is of order Ω² and we neglect it, v_y << v_z.)
  v_z(t) = -g_efft,  v_y(t) = -2Ω_xg_eff∫₀^tt'dt' = -Ω_xg_efft² = Ω sinθg_efft².
  y(t) = ∫₀^tv_y(t')dt' = Ω sinθg_efft³/3.
  h = ½g_eff t²,  t = (2h/g_eff)^½.
  deflection:  y(h) = (1/3)Ω sinθ(2h³/g_eff)^½, or
  y(h) = (1/3)Ω cosλ(2h³/g_eff)^½,
  The object is deflected eastward.