More Problems

Problem 1:

The matrix of the Hamitonian of a 3-state quantum mechanical system in the orthonormal basis {|u₁>, |u₂>, |u₃>}

.
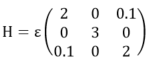(a)  Find the eigenvalues of this Hamiltonian and the normalized eigenvectors in this basis.
(b)  Assume at t = 0 the system is in the state u₁.  Find the probability that at t = t₁ a measurement will find the system in the state |u_i>, for i = 1, 2, 3.

Solution:

• Concepts:
  Eigenvalues and eigenvectors, the evolution operator
• Reasoning:
  E₂ = 3ε is one of the eigenvalues.  The corresponding eigenvector is |Φ₂> = |u₂> = .
  To find the other eigenvalues of H we diagonalize the matrix
   .
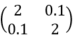• Details of the calculation:
  (2 - λ)² - 0.01 = 0,  λ = 2 ± 0.1.
  The energy eigenvalues are E₁ = 2.1ε with eigenvector |Φ₁> = ,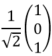
  and E₂ = 1.9ε with eigenvector |Φ₃> = .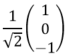
  
  (b)  |ψ(0)> = |u₁> = 2^-½(|Φ₁> + |Φ₃>).
  |ψ(t)> = 2^-½(|Φ₁>exp(-(i/ħ)E₁t) + |Φ₃>exp(-(i/ħ)E₃t))
  =  2^-1((|u₁> + |u₃>)exp(-(i/ħ)E₁t) + (|u₁> - |u₃>)exp(-(i/ħ)E₃t))
  = 2^-1(|u₁>(exp(-(i/ħ)E₁t) + exp(-(i/ħ)E₃t)) + |u₃>(exp(-(i/ħ)E₁t) - (exp(-(i/ħ)E₃t)).
  The probability that at t = t₁ a measurement will find the system in the state |u_i> is
  P(u_i) =|<u_i|ψ(t₁)>|².
  P(u₁) = ¼|(exp(-(i/ħ)E₁t) + exp(-(i/ħ)E₃t))|²
  =  ½(1 + cos((E₁ - E₃)t₁/ħ)) = cos²((E₁ - E₃)t₁/(2ħ)).
  = cos²(0.2εt₁/(2ħ)).
  P(u₂) = 0.
  P(u₃) = ¼|(exp(-(i/ħ)E₁t) - exp(-(i/ħ)E₃t))|²
  =  ½(1 - cos(E₁ - E₃)t₁/ħ)) = sin²(0.2εt₁/(2ħ)).

Problem 2:

Define what is meant by the term "stationary state" in quantum mechanics.  Why do we observe spontaneous transitions from excited stationary state?.

Solution:

• Concepts:
  The Schroedinger equation
• Reasoning:
  The Schroedinger equation is a non-relativistic equation.  It quantizes the electronic energy levels but not the electromagnetic field.
• Details of the calculation:
  A stationary state is an eigenstate of the energy operator iħ∂ψ(r,t)/∂t = Eψ(r,t) and therefore of the Hamiltonian H.  Stationary states can be written as ψ(r,t) = ψ(r) exp(-iEt/ħ), and |ψ(r,t)|² = ψ(r) exp(-iEt/ħ) ψ^*(r) exp(iEt/ħ) = ψ(r)ψ^*(r) = |ψ(r)|² is independent of time.  (Hence the name!)  The time-independent Schroedinger equation is the eigenvalue equation for H.
  To explain spontaneous emission we need quantum electrodynamics (QED), a relativistic quantum field theory which describes matter and light interaction by means of exchange of photons.
  The interaction of the radiation field and the electrons in an atom, which form two quantum systems, contains a term of the single-photon creation operator a^†, which does not vanish even if there is no photon present initially.  It is this term that makes atoms in excited states emit light, causing spontaneous transition.

Problem 3:

A particle is represented (at time t = 0) by the wave function

ψ(x,t) = A(a² - x²) if -a < x < a, ψ(x,t) = 0 otherwise.

(a)  Determine the normalization constant A.
(b)  What is the expectation value of x (at time t = 0)?
(c)  What is the expectation value of p (at time t = 0)?
(d)  Find the expectation value of x².
(e)  Find the expectation value of p².
(f)   Find the uncertainty in x (Δx).
(g)  Find the uncertainty in p (Δp).
(h)  Check that your results are consistent with the uncertainty principle.

Solution:

• Concepts:
  Postulates of quantum mechanics
• Reasoning:
  We use the given wave function to calculate the mean value and rms deviation of observables.
• Details of the calculation:
  (a)  We need  A²∫_-a^a(a² − x²)²dx = 2∫₀^a (a² − x²)²dx = A²16a⁵/15 = 1.
  A = √15 a^-5/2/4.
  (b)  <x> = ∫_-∞^∞|Ψ(x)|² x dx = A²∫_-a^a(a² - x²)² x dx = 0.
  |Ψ|² is even, x is odd and the integral is zero.
  (c)  <p> = (ħ/i)∫_-∞^∞Ψ*(x) (dΨ(x)/dx) dx = -A²(ħ/i)∫_-a^a2x (a² - x²) dx = 0.
  (d)  <x²> =  ∫_-∞^∞|Ψ(x)|² x² dx = A²∫_-a^a(a² - x²)² x² dx = a²/7.
  (e)  <p²> = -ħ²∫_-∞^∞Ψ*(x) (d²Ψ(x)/dx²) dx = A²ħ²∫_-a^a2(a² - x²) dx = (5/2)(ħ²/a²).
  (f)  Δx = (<x²> - <x>²)^½ = a/√7.
  (g)  Δp = (<p²> - <p>²)^½ = (5/2)^½(ħ/a).
  (h)  The uncertainty principle is satisfied.
  ΔxΔp = (a/√7)(5/2)^½(ħ/a) = (5/14)^½ħ > ħ/2.