More Problems

Problem 1:

(a)  Show that two Lagrangians L₁ and L_2, which differ only by the total derivative of a function of q and t, i.e.  L₂ = L₁ + df(q,t)/dt, describe the same motion for q.
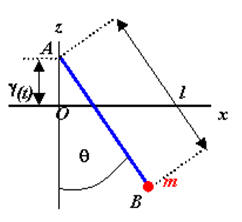
(b)  Find the Lagrangian and Hamiltonian of a pendulum consisting of a mass m attached to a massless rigid rod AB of length l free to move in a vertical plane.  The end A of the rod is forced to move vertically, so that its displacement from the fixed point O is a given function of time γ(t).  Gravity acts vertically downward.
(c)  Show that the vertical acceleration of the point A, d²γ(t)/dt², has the same effect on the equation of motion as a time varying gravitational field.

Solution:

• Concepts:
  Lagrange's equations
• Reasoning:
  L = T - U, H(q, p, t) = ∑_i(dq_i/dt)p_i - L.  
• Details of the calculation:
  (a)  Let L₁ be the Lagrangian of the system.
  Then d/dt(∂L₁/∂(dq/dt)) -  ∂L₁/∂q = 0 yields the equations of motion.
  Let L₂ = L₁ + df(q,t)/dt = L₁ + g, with g = df(q,t)/dt.
  The equations of motion are unchanged if d/dt(∂g/∂(dq/dt)) -  ∂g/∂q = 0.
  g = df/dt = ∂f/∂t + ∂f/∂q dq/dt.
  Remember:  q and dq/dt are independent variables.
  
  ∂g/∂(dq/dt) = ∂f/∂q.  d/dt(∂g/∂(dq/dt)) = d/dt(∂f/∂q).
  
  ∂g/∂q = ∂/∂q(df/dt) = ∂/∂q(∂f/∂t +  ∂f/∂q dq/dt) = ∂²f/∂t∂q + ∂²f/∂q² dq/dt  = d/dt(∂f/∂q).
  Therefore d/dt(∂g/∂(dq/dt)) -  ∂g/∂q = 0.
  
  (b)  L = T - U.
  z = γ - l cosθ,  x = l sinθ,  dz/dt = dγ/dt + l sinθ dθ/dt.  dx/dt = l cos dθ/dt.
  T = ½m((dz/dt)² + (dx/dt)²) = ½m((dγ/dt)² + l²(dθ/dt)²) + ml(dγ/dt)(dθ/dt) sinθ.
  U = -mg(lcosθ - γ).
  Constraint: γ = γ(t). 
  L(θ, dθ/dt) = ½m((dγ/dt)² + l²(dθ/dt)²) + ml(dγ/dt)(dθ/dt) sinθ + mg(lcosθ - γ).
  
  p_θ = ∂L/∂(dθ/dt) = ml² dθ/dt + ml(dγ/dt)sinθ.
  H = p_θ(dθ/dt) - L =  -½m(dγ/dt)² + ½ml²(dθ/dt)² + U.
  dθ/dt = (p_θ - ml(dγ/dt)sinθ)/(ml²).
  H(θ,p_θ) = (p_θ - ml(dγ/dt)sinθ)²/(2ml²) - ½m(dγ/dt)² + U.
  
  (c)  d/dt(∂L/∂(dθ/dt)) = ml²d²θ/dt² + mld²γ/dt²sinθ + ml(dγ/dt)cosθ dθ/dt/
  ∂L/∂θ = ml(dγ/dt)(dθ/dt) cosθ - mglsinθ/
  ml²d²θ/dt² + mld²γ/dt²sinθ + ml(dγ/dt)cosθ dθ/dt - ml(dγ/dt)(dθ/dt) cosθ + mglsinθ = 0.
  d²θ/dt² = -d²γ/dt²sinθ/l - gsinθ/l = -g(t)sinθ/l.  g(t) = g + d²γ/dt².
  
  Think about:  Is H conserved?  Is H the total energy of the system?

Problem 2:

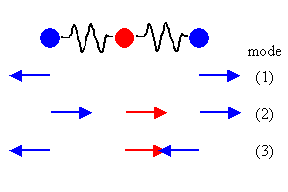
Find the normal, longitudinal modes of vibration for three masses connected by identical springs of spring constant k.  The masses are collinear.  The end masses have mass m, while the inner mass has mass 2m.
(a)  Calculate the normal modes of the system.
(b)  Describe the relative motion of the particles for each normal mode.

Solution:

• Concepts:
  Coupled oscillations, normal modes
• Reasoning:
  We are asked to find the normal modes of coupled harmonic oscillators.
• Details of the calculation:
  (a)  The kinetic energy is T = ½[m(dx₁/dt)² +  2m(dx₂/dt)² +  m(dx₃/dt)²],
  and the potential energy is U = (k/2)[(x₂ - x₁)² + (x₃ - x₂)²].
  U = (k/2)[x₁² + 2x₂² + x₃² - x₁x₂ - x₂x₁ - x₂x₃ - x₃x₂].
  The x_i are the displacements from the equilibrium positions.  We use the x_i as our generalized coordinates q_i.
  The Lagrangian is L = T - U.  This can be put into the form
  L = ½∑_ij[T_ij(dq_i/dt)(dq_j/dt) - k_ijq_iq_j]  with T_ij = T_ji,  k_ij = k_ji. 
  Here T₁₁ = T₃₃ = m, T₂₂ = 2m, T_ij(i≠j) = 0,
  k₁₁ = k₃₃ = k, k₂₂ = 2k, k₁₂ = k₂₁ = k₂₃ = k₃₂ = -k, k₁₃ = k₃₁ = 0.
  Solutions of the form x_j = Re(A_je^{iω t}) can be found.  For solutions of this form the equations of motion reduce to
  

   

  	k-ω2m	-k	0
  	-k	2k-2ω2m	-k
  	0	-k	k-ω2m

  	A1
  	A2
  	A3

    = 0.

  
  

  
  
  We can find the ω² from det(k_ij-ω ²T_ij) = 0.  For a system with n degrees of freedom, n characteristic frequencies ω_a can be found.  Our system has 3 degrees of freedom.

   

  	k-ω2m	-k	0
  	-k	2k-2ω2m	-k
  	0	-k	k-ω2m

    = 0.

  
  

  
  2(k-ω²m)³ - 2k²(k-ω²m) = 0.
  Solution 1: k-ω²m = 0,  ω = (k/m)^½.
  Solution 2: k-ω²m ≠ 0, then (k-ω²m)² = k², (k-ω²m) = ±k.
  For (k-ω²m) = +k, ω = 0.
  Solution 3: (k-ω²m) = -k, ω = (2k/m)^½.
  
  (b)  The displacements for each mode are determined from the equations of motion.
  Solution 1: ω = (k/m)^½.
  Equation 1 yields kA₂ = 0, equation 2 then yields kA₁ + kA₃ = 0.
  A₁ = - A₃, A₂ = 0, the central mass is stationary, m₁ and m₃ move in opposite directions with equal amplitudes.
  Solution 2: ω = 0.
  A₁ = A₂ = A₃, translation of the CM, no relative motion.
  Solution 3: ω = (2k/m)^½.
  Equation 1 yields -kA₁ - kA₂ = 0, A₁ = -A₂.
  Equation 3 yields -kA₂ - kA₃ = 0, A₃ = -A₂.
  A₁ = A₃ = -A₂, the central mass move in a direction opposite to the direction of the outer masses.  All masses oscillate with equal amplitudes.
  

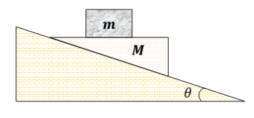
Problem 3:

A wedge of mass M is moving along a frictionless slope. The slope is fixed to the ground and the slope angle is θ.
The top surface of the wedge M remains horizontal and a cube with mass m is sitting on top of the wedge.  There is also no friction between the cube m and the wedge M.

(a)  Find the relative acceleration between m and M.
(b)  Find the magnitude of the normal force N between M and the slope.

Solution:

• Concepts:
  Lagrangian Mechanics or Newton's laws
• Reasoning:
  All forces, except the forces of constraint, are derivable from a potential.  The Lagrangian formalism is well suited for such a system because we do not have to solve for the forces of constraint or explicitly eliminate them from the equations of motion.
• Details of the calculation:
  Put the origin of the coordinate system at the right edge of the slope, and let the x-axis point to the left and the y-axis point up.
  
  Lagrangian Mechanics
  (a)  L = T - U.
  T = T_wedge + T_m = ½M(dx/dt)² + ½(m + M)[(dy/dt)²,  U = (m + M)gy.
  y = x tanθ.
  L = ½(M + Mtan²θ + mtan²θ)(dx/dt)² - (m + M)gx tanθ.
  (M + Mtan²θ + mtan²θ)dx²/dt² + (m + M)g tanθ = 0.
  dx²/dt² = -(m + M)g tanθ /(M + Mtan²θ + mtan²θ).
  dy²/dt² = -(m + M)g tan²θ /(M + Mtan²θ + mtan²θ).
  dx²/dt² is the relative acceleration between m and M.
  
  (b)  Nsinθ = -M dx²/dt².
  N = (M/cosθ)(m + M)g /(M + Mtan²θ + mtan²θ)
  is the magnitude of the normal force N between M and the slope.
  
  Newton's laws
  Let N₁ be the magnitude of the normal force between the slope and the wedge and N₂ the magnitude of the normal force between the wedge and the cube.
  (a)  Wedge: 
  -Mg + N₁cosθ - N₂ = M dy²/dt²,  - N₁sinθ = M dx²/dt² = (M/tanθ) dy²/dt²_.
  Inserting:  -Mg - (M/tan²θ) dy²/dt² - N₂ = M dy²/dt².
  Cube:
  dy²/dt² = -g + N₂/m.
  Combining:  -Mg - (M/tan²θ) dy²/dt² - m dy²/dt² -mg  = M dy²/dt².
  dy²/dt² = -(m + M)g tan²θ /(M + Mtan²θ + mtan²θ).
  dx²/dt² = -(m + M)g tanθ /(M + Mtan²θ + mtan²θ).
  
  (b)  -N₁sinθ = (M/tanθ) dy²/dt²_.
  N₁ = (M(m + M)g/cosθ) /(M + Mtan²θ + mtan²θ).