Problem 1:

A uniform density disk of radius R = 0.1 m and mass M = 2 kg is spinning about a perpendicular axis through its center with initial angular speed ω₀ = dθ/dt|_{t = 0} = 4/s.  At t = 0 and θ = 0  a torque τ = Asinθ with A = 0.05 Nm is applied for half a revolution.  Find the final angular speed ω_f.

Solution:

• Concepts:
  Rotational motion, solving a differential equation
• Reasoning:
  τ = Id²θ/dt²,  d²θ/dt² = (A/I)sinθ.
• Details of the calculation:
  (dθ/dt) d²θ/dt² = (dθ/dt) (A/I)sinθ.
  Let dθ/dt = x.
  x dx/dt = ½dx²/dt= (dθ/dt) (A/I)sinθ.
  Integrate:
  ½∫(dx²/dt) dt = ½∫dx²= (A/I)∫ (dθ/dt) sinθ dt = (A/I)∫ dθ sinθ.
  ½x² = ½(dθ/dt) ² = -(A/I) cosθ + constant
  dθ/dt = (-(2A/I) cosθ + C)^½ with C determined by the initial conditions.
  ω₀² = (-(2A/I) + C),  C = ω₀² + 2A/I.
  after half a revolution, θ = π, ω_f = (4A/I + ω₀²)^½.
  I = ½MR² = 10^-2 kgm².  4A/I = 20, ω_f = 6/s.

Problem 2:

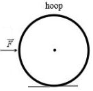A hoop of mass M and radius R rests on a perfectly rough floor.
At t = 0 a constant force F is applied to the wheel as shown in the figure.. 
Find the resulting acceleration of the wheel.

Solution:

• Concepts:
  Rolling
• Reasoning:
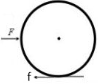  The force of static friction, f,  preventing the contact point from slipping, opposes the applied force.  It also exerts a torque on the wheel.
• Details of the calculation:
  F - f = Ma.   τ = fR = Iα = Ia/R.  f = Ia/R² = Ma.
  F = 2Ma,  a = F/2M, in the direction of F.

Problem 3:

Write the equation of motion for a classical mass-point in a rotating coordinate system with varying angular velocity Ω. Identify the centrifugal, and Coriolis, and Euler contributions in the equation of motion.

Solution:

• Concepts:
  Motion in a non-inertial frame
• Reasoning:
  A rotating coordinate system is a non-inertial frame.  Fictitious forces appear.
• Details of the calculation:
  The relationship between the time derivatives of any vector A in a fixed, inertial frame and in a frame rotating with angular velocity Ω is
  (dA/dt)_fixed = (dA/dt)_rotating + Ω × A.
  Therefore:
  (dr/dt)_fixed = (dr/dt)_rotating + Ω × r.
  The relationship between the velocity v_i in the inertial frame and the velocity v in a frame rotating with angular velocity Ω is
  v_i = v + Ω × r.
  Differentiating again we have
  (dv_i/dt)_fixed = (dv/dt)_fixed + Ω × (dr/dt)_fixed + (dΩ/dt)_fixed × r.
  Inserting (dr/dt)_fixed from above we have
  (dv_i/dt)_fixed = (dv/dt)_fixed + Ω × v + Ω × (Ω × r)  + (dΩ/dt)_fixed × r.
  F_i = m(dv_i/dt)_fixed = m(dv/dt)_fixed + mΩ × v + mΩ × (Ω × r) + m(dΩ/dt)_fixed × r.
  Now we use
  (dv/dt)_fixed = (dv/dt)_rotating + Ω × v.
  F_i  = m(dv/dt)_rotating + 2mΩ × v + mΩ × (Ω × r) + m(dΩ/dt)_fixed × r
  to obtain the equations of motion in the rotating frame.
  The equations of motion in the rotating frame therefore are
  (dv/dt)_rotating = F_i - 2mΩ × v - mΩ × (Ω × r) - m(dΩ/dt)_fixed × r.
  2m(v × Ω) = -2m(Ω × v) = Coriolis contribution.
  m(Ω × r) × Ω = -mΩ × (Ω × r) = centrifugal contribution.
  r × m(dΩ/dt)_fixed = -m(dΩ/dt)_fixed × r = Euler contribution.