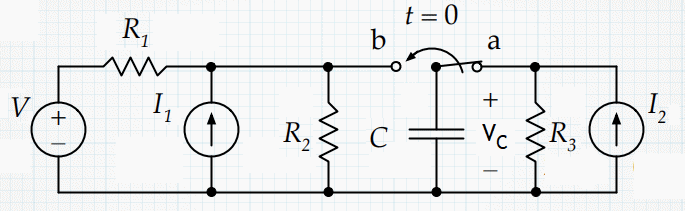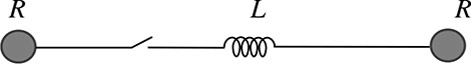Problem 1:
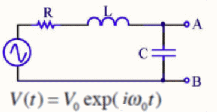
Consider the LCR circuit shown. The circuit is driven by a sinusoidal
voltage V(t) = V0exp(iωt), where ω = ω0 = 1/√(LC) is the
resonant frequency of the circuit.
(a)
Solve for the current I(t) in the circuit.
(b)
Find the voltage VAB(t) where VAB = VA - VB.
Problem 2:
(a) Derive the expression and calculate the capacitance
per unit length for a piece of coaxial cable in SI units. The coaxial cable has
a diameter of an inner wire of 1 mm and an inner diameter (ID) of an outer
shield of 5 mm. The dielectric constant of the insulator between the two
conductors is κe = 1.5. The
dielectric permeability of the free space is ε0
= 8.8*10-12 F/m.
(b) Derive the expression and calculate the inductance for this cable in
SI units, assuming that the relative magnetic permeability is unity κm = 1. The magnetic permeability
of the free space is
μ0 = 4π*10-7 H/m. For problems (a) and (b) assume
that the skin depth of the wire and shield are zero (a high-frequency limit).
(c) Derive the expression and calculate the wave impedance for this
cable.
Problem 3:
In the circuit shown, the switch has been in position a for a very long time.
At t = 0, it abruptly switches to position b. Find the expression
for the capacitor voltage VC as a function of time.
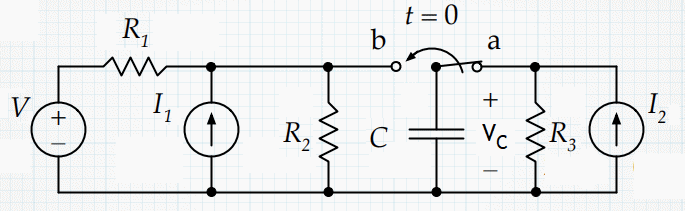
Let V = 50 V, R1 = 500 Ω, R2 = 125 Ω, R3
= 25 Ω, C = 2*10-6 F, I1 = 0.1 A, and I2 = 0.2
A.
Problem 4:
In the circuit shown below, two conducting spheres of radius R each are
located far away from each other and are connected by thin wires through a
solenoid with inductance L. Initially, one of the spheres is charged and
the other is neutral. How long after the switch is closed do the charges
on the spheres become equal?
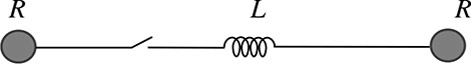
Problem 5:
Consider the circuit shown.
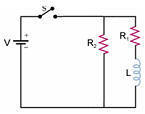
Let V = 50 V, R1 = 10 Ω, R2 = 100 Ω, and L = 50 H.
All circuit elements are ideal and no current flows before the switch is
closed.
(a) After the switch is closed at t = 0, find the current I flowing through
the switch as a function of time.
(b) After 8 s the switch is opened again. Right after the switch is opened,
what is the voltage across R2 and across the switch?