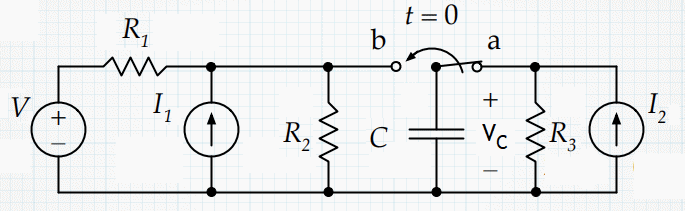Problem 1:
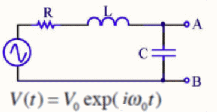
Consider the LCR circuit shown. The circuit is driven by a sinusoidal
voltage V(t) = V0exp(iωt), where ω = ω0 = 1/√(LC) is the
resonant frequency of the circuit.
(a)
Solve for the current I(t) in the circuit.
(b)
Find the voltage VAB(t) where VAB = VA - VB.
Solution:
- Concepts:
AC circuits
- Reasoning:
We are asked to analyze an AC circuit.
-
Details of the calculation:
(a)
V = IZ.
Z = R + iωL + 1/(iωC) = R + i(ωL - 1/(ωC)) = (R2 + (ωL - 1/(ωC))2)½exp(iφ).
φ = tan-1((ω2LC - 1)/(ωRC)).
I = V/Z = [V0/(R2 + (ωL - 1/(ωC))2)½]exp(i(ωt
- φ)).
If ω = ω0 = 1/√(LC) then I = [V0/R]exp(iω0t).
(b)
VAB = I*ZC = [V0/R]exp(iω0t)ZC
= -i[V0/(ωRC)]exp(iω0t) = V0/(ωRC)] exp(iωt
- π/2).
Problem 2:
(a) Derive the expression and calculate the capacitance
per unit length for a piece of coaxial cable in SI units. The coaxial cable has
a diameter of an inner wire of 1 mm and an inner diameter (ID) of an outer
shield of 5 mm. The dielectric constant of the insulator between the two
conductors is κe = 1.5. The
dielectric permeability of the free space is ε0
= 8.8*10-12 F/m.
(b) Derive the expression and calculate the inductance for this cable in
SI units, assuming that the relative magnetic permeability is unity κm = 1. The magnetic permeability
of the free space is
μ0 = 4π*10-7 H/m. For problems (a) and (b) assume
that the skin depth of the wire and shield are zero (a high-frequency limit).
(c) Derive the expression and calculate the wave impedance for this
cable.
Solution:
- Concepts:
Gauss' law, Ampere's law, ladder circuits
- Reasoning:
The problem has cylindrical symmetry. Treat the circuit as an infinite
ladder network with characteristic impedance Z.
-
Details of the calculation:
(a) For a given charge on the cylinder we find D from Gauss' law for
D.
We then use D to find E, V, and C. Assume the inner cylinder carrier a free
charge per unit length λf.
D = (λf/2πr)(r/r) (a < r < b) from Gauss' law for
D.
Here r is a cylindrical coordinate and we use SI units.
E = (λf/2πεr)(r/r).
ΔV = ∫abEdr = ∫ab(D/ε)dr = (λf /(2πε))ln(b/a).
C' = λf/ΔV = (2πε)/ln(b/a) is the capacitance per unit length. Here
ε = 1.5, a = 0.5 mm and b = 2.5 mm.
C' = 53 pF/m.
(b) Now assume the inner
cylinder carries a free current I.
We find the magnetic field produce by the current from Ampere's law for H,
use H to find B, and solve
½LI2 = (1/(2μ))∫ B2dV for the self inductance
L.
Ampere's law: H = I/(2πr) between the conductors, B
= μI/(2πr) B encircles the inner conductor
according to the right hand rule.
Uper unit lngth = ½L'I2 = (μI2/(4π)) ∫ab
(1/r) dr = (μI2/(4π)) ln(b/a). Here μ = μ0.
L' = (μ/(2π)) ln(b/a) is the self-inductance per unit length. L' = 3.22*10-7
H/m.
(c) Treat the circuit as an infinite ladder network
with characteristic impedance Z.
Since the ladder is infinite, the impedance Z will not change if an additional
section is added to the front of ladder.
An equivalent
network with impedance Z is shown in the figure.

Here Z1 = iωL'dl
and Z2 = -i/(ωC'dl).
Z = Z1 + ZZ2/(Z + Z2) = iωL'dl
- iZ/(ωC'dl)/ (Z - i/(ωC'dl))
= iωL'dl + Z/(iωC'dlZ
+ 1).
Since dl -->
0, we may expand (1 + iωC'dlZ)-1 =
(1 - iωC'dlZ).
Z = iωL'dl + Z(1 - iωC'dlZ).
0 = L' - C'Z2. Z2 = L'/C'.
The wave impedance of the cable is (L'/C')½ = [ln(b/a)/(2π)] (μ/ε)½
= 78 Ω.
Problem 3:
In the circuit shown, the switch has been in position a for a very long time.
At t = 0, it abruptly switches to position b. Find the expression
for the capacitor voltage VC as a function of time.
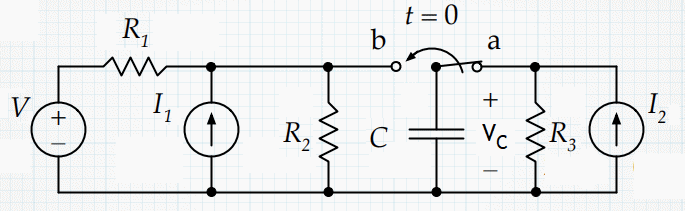
Let V = 50 V, R1 = 500 Ω, R2 = 125 Ω, R3
= 25 Ω, C = 2*10-6 F, I1 = 0.1 A, and I2 = 0.2
A.
Solution:
- Concepts:
RC circuits
- Reasoning:
For t < 0, the portion of the circuit to the left of the switch is not connected to the capacitor. The circuit to the right
of the switch determines VC.
Since the switch was in position a for a long time, the capacitor current is
zero and VC = I2R3 = 5 V.
After the flip, the circuit to the left will determine VC.
- Details of the calculation:
For t > 0, the portion of the circuit to the right of the switch is not
connected to the capacitor.
The Thevenin voltage VTH is an ideal voltage source equal to the open circuit
voltage at the terminals. The Thevenin resistance RTH is the resistance
measured at the terminals with all voltage sources replaced by short circuits
and all current sources replaced by open circuits.
Assume the negative terminal of the voltage source is at ground.
Assume that point b is at voltage Vb = VTh.
Use Kirchhoff's junction rule for the node above R2.
(V - Vb)R + I1 = Vb/R2.
The Thevenin equivalent voltage and resistance of the circuit on the left
are
VTh = VR2/(R1 + R2) + I1R1R2/(R1
+ R2) = 20 V.
RTh = R1R2/(R1 + R2)
= 200 Ω.

Now we just have a simple RC circuit.
VC(t) = Vf - (Vf - Vi)exp(-t/RC)
= 20V - 15Vexp(-t/2*10-4s).
The capacitor starts at 5 V and charges to 20 V with a time constant of 200
μs.
Problem 4:
In the circuit shown below, two conducting spheres of radius R each are
located far away from each other and are connected by thin wires through a
solenoid with inductance L. Initially, one of the spheres is charged and
the other is neutral. How long after the switch is closed do the charges
on the spheres become equal?
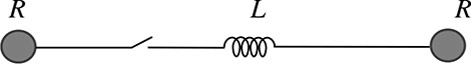
Solution:
- Concepts:
LC tank circuits
- Reasoning:
We treat the spheres as capacitors, each with Csp = 4πε0R.
The capacitors are in series (the connection is at infinity), so we have an LC tank
circuit with C = Csp/2 = 2πε0R.

The circuit is not
neutral, it carries an excess charge Q approximately uniformly distributed over the two
spheres. Denote the oscillating charge by Q' .
-
Details of the calculation:

Kirchhoff's loop rule:
Q'/C + LdI/dt = 0. d2Q'/dt2 + Q'/(LC) = 0.
Q'
= (Q/2)cosωt, ω = (LC)-½.
Q/2 is the oscillating charge on the initially charged sphere.
The oscillation period is T = 2π/ω = 2π(LC)½ =
(2π)3/2(ε0RL)½.
The charges on the spheres become equal for the first time after one quarter
period, T/4 = (π/2)(2πε0RL)½
Problem 5:
Consider the circuit shown.
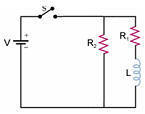
Let V = 50 V, R1 = 10 Ω, R2 = 100 Ω, and L = 50 H.
All circuit elements are ideal and no current flows before the switch is
closed.
(a) After the switch is closed at t = 0, find the current I flowing through
the switch as a function of time.
(b) After 8 s the switch is opened again. Right after the switch is opened,
what is the voltage across R2 and across the switch?
Solution:
- Concepts:
Transient RL circuits, Kirchhoff's rules
- Reasoning:
We are asked to analyze the transient behavior of an RL circuit.
- Details of the calculation:
(a) Let I1 flow through R1 and I2 flow through R2.
Assume the directions for I1 and I2 are from top to
bottom.
V - R1I1 - LdI1/dt = 0, V - I2R2
= 0, I = I1 + I2.
I2 = V/R2, dI1/dt = V/L - R1I1.
I1(t) = (V/R1)[1 - exp(-R1t/L)].
I = 0.5 A + 5 A[1 - exp(-(0.2/s)t)].
(b) Right after the switch is opened I = 5 A[1 - exp[(-0.2/s)8 s)] = 4 A of
current flow through R2 from the bottom to the top. The voltage
across R2 is 400 V, Vbottom - Vtop = 400 V.
The voltage across the switch is 450 V.