Problem 1:

A mass m is connected by a string of negligible mass to a pulley of mass M = 6m and radius R as shown.  The pulley has uniform mass density.  Assume that at t = 0 the mass is at z = 0 and θ = 0.  For the time the mass is falling, find the equations of motion for z and θ and the forces of constraint using the method of Lagrange multipliers.

Solution:

• Concepts:
  Lagrange's Equations, Lagrange multipliers
  d/dt(∂L/∂(dq_k/dt)) -  ∂L/∂q_k = ∑_lλ_la_lk,    Σ_k a_lk dq_k + a_lt dt =  0.
• Reasoning:
  The problem requires us to use the method of Lagrange multipliers. 
  The coordinate z denotes the distance the mass has fallen, the coordinate θ denotes the angle through which the pulley has turned.
  Then L = m(dz/dt)²/2 + I(dθ/dt)²/2 + mgz.
  The equation of constraint is z = Rθ, dz = Rdθ, dz - Rdθ = 0.
  There is only one equation of constraint, so we can drop the index k.
  a_z = 1,  a_θ = -R.
• Details of the calculations:
  The equations of motion are
  md²z/dt² - mg = λ,
  Id²θ/dt²  = -Rλ.
  dz - Rdθ = 0.
  Solving these 3 equations we obtain
  (m + I/R²)d²z/dt² = mg.
  d²z/dt² = mg/(m + 0.5M) = g/4, since I = MR²/2.  and M = 6m.
  λ = -3mg/4 is the force of constraint acting on m in the z-direction, it is the tension in the string pulling upwards on m.  The - sign indicates that the force of constraint is acting upwards.
  -Rλ = 3mgR/4 is the torque acting on the disk.  It is the generalized force of constraint associated with the coordinate θ.  The torque is pointing into the page.

Problem 2:

A uniform hoop of mass m and radius r rolls without slipping on a fixed cylinder of radius R as shown in the figure.  The only external force is that of gravity.  If the hoop starts rolling from rest on top of the big cylinder, find, by the method of Lagrange multipliers, the point at which the hoop falls off the cylinder.

Solution:

• Concepts:
  Lagrange multipliers
• Reasoning:
  The Lagrange multiplier technique yields the radial force of constraint.  The contact between the hoop and the cylinder will be lost when the radial force of constraint changes sign.  The cylinder cannot pull.
• Details of the calculation:
  To find the radial force of constraint, we let R, θ₁ and θ₂ be the generalized coordinates.
  They are connected by constraints of the form Σ_k a_lk dq_k + a_lt dt = 0.
  We have two equations of constraint.
  R = R₁, dR = 0, therefore we can choose a_1R = 1, a_1θ1 = a_1θ2 =  0.
  (We use R₁ for the radius of the fixed sphere, to distinguish from the generalized coordinate R.)
  dθ₂ = dθ₁(R + r)/r, therefore we can choose a_2R = 0, a_2θ1 = 1, a_2θ2 = -r/(R + r).
  (Note:  θ₂ ≠ θ₁(R + r)/r until R is fixed.  If we let R be a coordinate then we only have a constraint equation connecting the differentials of the coordinates.)
  
  The three equations of motion are
  d/dt(∂L/∂(dq_k/dt)) -  ∂L/∂q_k = ∑_lλ_la_lk,
  which have to be solve together with the two equations of constraint.
  We have five equations and five unknowns, R(t), θ₁(t), θ₂(t), λ₁ and λ₂. 
  
  T = ½m(r + R)²(dθ₁/dt)² + ½mr²(dθ₂/dt)² + ½m(dR/dt)².  U = mg(r + R)cosθ₁.
  L = T - U.
  ∂L/∂(dR/dt)  = mdR/dt,  d/dt(∂L/∂(dR/dt)) = md²R/dt², 
  ∂L/∂R = m(r + R)(dθ₁/dt)² - mgcosθ₁.
  d/dt(∂L/∂(dR/dt)) - ∂L/∂R = λ₁a_1R + λ₂a_2R
  (1)  md²R/dt² - m(r + R)(dθ₁/dt)² + mgcosθ₁ = λ₁,
  
  ∂L/∂(dθ₁/dt) = m(r + R)²(dθ₁/dt), 
  d/dt(∂L/∂(dθ₁/dt)) = m(r + R)²d²θ₁/dt² +  2m(r + R)(dθ₁/dt)(dR/dt),
  ∂L/∂θ₁ = mg(r + R)sinθ₁.
  d/dt(∂L/∂(dθ₁/dt)) - ∂L/∂θ₁ = λ₁a_1θ1 + λ₂a_2θ1, 
  (2)  m(r + R)²d²θ₁/dt² + 2m(r + R)(dθ₁/dt)(dR/dt) - mg(r + R)sinθ₁ = λ₂. 
  
  ∂L/∂(dθ₂/dt) = mr²(dθ₂/dt), 
  d/dt(∂L/∂(dθ₂/dt)) = mr²d²θ₂/dt²,
  ∂L/∂θ₂ = 0.
  d/dt(∂L/∂(dθ₂/dt)) - ∂L/∂θ₂ = λ₁a_1θ2 + λ₂a_2θ2, 
  (3)  mr²d²θ₂/dt² = -λ₂r/(r + R). 
  
  Constraints:
  dR/dt = 0 --> d²R/dt² = 0, r = R₁. 
  dθ₂ = dθ₁(R + r)/r --> d²θ₂/dt² = ((R₁ + r)/r)d²θ₁/dt².
  Therefore
  from (1):  -m(r + R₁)(dθ₁/dt)² + mgcosθ₁ = λ₁.
  from (2):  m(r + R₁)²d²θ₁/dt² - mg(r + R₁)sinθ₁ = λ₂. 
  from (3):  md²θ₁/dt² = -λ₂/(r + R₁)².
  
  Combining the last two equations we have
  2m(r + R₁)²d²θ₁/dt² - mg(r + R₁)sinθ₁ = 0.
                            
  Contact is lost when λ₁ = 0.  (The normal force cannot pull.)
  Then  dθ₁/dt = [gcosθ₁/(r + R₁)]^½.
  
  To find  dθ₁/dt as a function of θ₁ we need to solve the differential equation
  2m(r + R₁)²d²θ₁/dt² - mg(r + R₁)sinθ₁ = 0,
  or
  d²θ₁/dt² = gsinθ₁/(2(r + R₁))
  for dθ₁/dt.
  Denote dθ₁/dt = f(θ₁).
  df(θ₁)/dt = [df(θ₁)/dθ₁]f(θ₁) = ½df²(θ₁)/dθ₁ = gsinθ₁/(2(r + R₁)) .
  f²(θ₁) = A - (g/(r + R₁))cosθ₁.
  dθ₁/dt =  [A - (g/(r + R₁))cosθ₁]^½.
  
  Initial conditions:  dθ₁/dt = 0 for θ₁ = 0, A = g/(r + R₁).
  dθ₁/dt =  [g/(r + R₁) - g cosθ₁/(r + R₁)]^½.
  The hoop falls off when gcosθ₁/(r + R₁)  = g/(r + R₁) - gcosθ₁/(r + R₁),
  cosθ₁  = (1 - cosθ₁),
  or cosθ₁ = ½, θ₁ = 60^o.
  
  Comments:  (not part of the asked for solution)
  
  Finding λ₁:
   -m(r + R₁)(dθ₁/dt)² + mgcosθ₁ = λ₁.
   -m(r + R₁)[(g/(r + R₁) - gcosθ₁/(r + R₁)] + mgcosθ₁ = λ₁.
   mg(2cosθ₁ - 1) = λ₁.
  λ₁a_1r = F_r, F_r =  mg(2cosθ₁ - 1) is the reaction (normal) force of the cylinder on the hoop.
  
  Finding λ₂:
  md²θ₁/dt² = -λ₂/(r + R₁)².
  m[g/(2(r + R₁))sinθ₁] = -λ₂/(r + R₁).²
  mg sinθ/2 = -λ₂/(r + R₁).
  What is the significance of λ₂?
  mr²d²θ₂/dt² = -λ₂r/(r + R₁)².
  -λ₂r/(r + R₁)² = mgr sinθ₁/2 is the generalized force associated with the coordinate θ₂.  Since θ₂ is an angle, the generalized force is a torque. Rolling implies static friction.  The force of static friction exerts a torque about the center of the hoop.
  mgr sinθ₁/2 = τ_θ2.
  Note:  The λs are not unique, but the formalism yields unique generalized forces of constraint.

Problem 3:

A particle of mass m is acted on by an attractive force whose potential is given by U(r) = -Ar^-4.   It is incident from infinity with an initial velocity v_∞.  Sketch the effective potential of the particle U_eff(r).  Find the total cross section for capture of the particle.

Solution:

• Concepts:
  Motion in a central potential
• Reasoning:
  In a central potential the energy E and the angular momentum M are conserved. 
• Details of the calculation:
  E = ½m(dr/dt)² + U_eff(r) = ½mv_∞².    M = mv_∞b,  b = impact parameter.
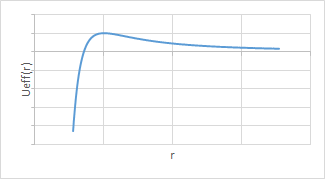
  U_eff(r) = M²/(2mr²) - A/r⁴.
  U_eff(r) --> 0 as r --> ∞.
  U_eff(r) --> -∞ as r --> 0.
  U_eff(r) has a maximum at r₀ such that dU_eff(r)/dr|_r0 = 0.
  
   

  -M²/(mr₀³) + 4A/r₀⁵ = 0,  r₀ = (4Am/M²)^½.
  U_eff(r₀) = M⁴/(16Am²).
  The condition for capture is ½mv_∞² > M⁴/(16Am²),
  ½mv_∞² > (mv_∞b)⁴/(16Am²),  b⁴ < 8A/(mv_∞²).
  σ_capture = πb² = (2π/v_∞)*(2A/m)^½.

Problem 4:

A beam of particles of mass m and non-relativistic kinetic energy E is scattered from a central potential.  The potential energy of a particle is U = -U₀,  for r < a, U = 0 for r > a.
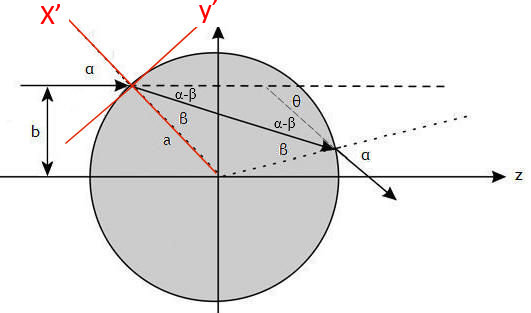
(a)  Show that the scattering produced by such a potential is identical to the refraction of light rays by a sphere of radius a and relative index of refraction n = ((E + U₀)/E)^½, i.e. show that sinα/sinβ = n, where α and β are defined in the diagram.

(b)  Show that the classical differential scattering cross section for this potential is
σ(θ) = dσ/dΩ = [n²a²/(4 cos(θ/2))](n cos(θ/2) - 1)(n  - cos(θ/2))/(1 + n² - 2n cos(θ/2))².

Solution:

• Concepts:
  The scattering cross section, scattering from a spherically symmetric potential
• Reasoning:
  The potential has spherical symmetry.  As the potential changes abruptly ar r = a, the tangential component of the momentum of the particles does not change.
• Details of the calculation:
  (a)  Define a coordinate system with a x' and a y' axis as shown.
  
  p² = p_x² = p_x'² + p_y'² at r = ∞.
  As the particle enters the region of non-zero potential, p_y' = constant since ∂U/∂y' = 0.
  E = p²/(2m) = p'²/(2m) - U₀.  (energy conservation)
  sinα/sinβ = (p_y'/p)/(p'_y'/p') = p'/p = ((E + U₀)/E)^½ = n.
  
  (b)  We need to find the impact parameter b as a function of θ or vice versa.
  Let a be the radius of the sphere.
  b = a sinα .  b² = a² sin²α.
  Geometry: θ = 2(α - β).
   
  sinβ/sinα = sin(α - θ/2)/sinα = cos(θ/2) - cotα sin(θ/2) = 1/n.
  cos(θ/2)/sin(θ/2) - 1/(nsin(θ/2))  = cotα.
  Use this to write b² in terms of θ.
  sin²α = 1/(cot²α + 1).
  cot²α + 1 = (n cos(θ/2) - 1)²/(n²sin²(θ/2)) + 1.
  1/(cot²α + 1) = n²sin²(θ/2)/[(n cos(θ/2) - 1)² + n²sin²(θ/2)]
  =  n²sin²(θ/2)/(n² + 1 - 2n cos(θ/2)).
  b² = a²/(cot²α + 1) = a²n²sin²(θ/2)/(n² + 1 - 2n cos(θ/2)).
  
  σ(θ) =|(b/sinθ)(db/dθ)|.  
  db²/dθ = 2b db/dθ
  = a²n²sin(θ/2)(cos(θ/2) + n²cos(θ/2) - ncos²(θ/2) - n)/(1 + n² - 2n cos(θ/2))².
  sinθ = 2sin(θ/2)cos(θ/2).
  σ(θ) = [n²a²/(4 cos(θ/2))](n cos(θ/2) - 1)(n  - cos(θ/2))/(1 + n² - 2n cos(θ/2))².

Problem 5:

In a scattering experiment, a beam of particles of mass m and energy E is sent towards a target.  The number of particles scattered per unit area per unit time into a specific direction is measured.  The potential energy function U(r) is that of a central attractive potential with a repulsive core.

(a)  Give the definition of the differential scattering cross section dσ/dΩ in terms of the impact parameter b and the scattering angle θ.
(b)  Relate the impact parameter b to the angular momentum, and thus find the dependence of θ(b) on U(r) and b in the form of an integral.
(c)  What is the value of the scattering angle θ for the special cases b = 0 and b = ∞?
(d)  Show that θ should become negative for suitable E and b.
(e)  Given the result of (d)  does the differential cross section ever diverge for any value of b?  Explain!

This problem just asks for definitions and reasoning, not for calculations.

Solution:

• Concepts:
  The scattering cross section, scattering from a spherically symmetric potential
• Reasoning:
  We are asked to think qualitatively about properties of the scattering cross section.
• Details of the calculation:
  (a)  σ(θ) =|(b/sinθ)(db/dθ)|.
  (b)  M = mv₀b = b(2mE)^½,  θ = π - 2φ₀ for a repulsive potential, 
  φ₀ = b∫₀^umaxdu/[1 - b²u² - U(u)/E]^½, with u = 1/r.
  E =  b²Eu²_max + U(u_max) yields u_max.
  (c)  b = 0 yields  φ₀ = 0, θ = π.  (The particle scatters backward, M = 0.)
  b = ∞ yields φ₀ = π/2, θ = 0.  (The particle is out of range of the scattering potential.)
  (d)  If we choose the impact parameter and the energy such that r_min = 1/u_max is greater than the value of r where the potential energy U(r) has a minimum, then the particle never sees the repulsive core and is scattered by an attractive potential, θ = π - 2φ₀ is negative.
  (e)  If we decrease the impact parameter, r_min decreases, the particle will see the repulsive core and θ will become positive.  For some finite impact parameter we will therefore have θ = 0, and σ(θ) diverges.