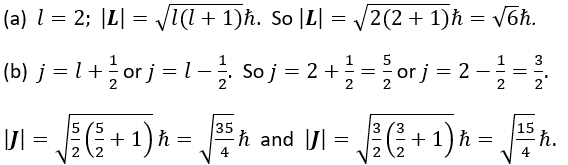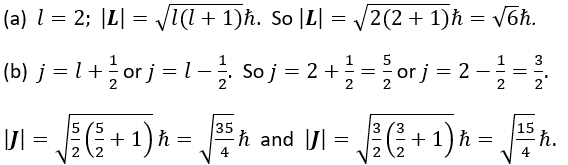Assignment 8

Problem 1:

An electron is in a state with l = 2 in an atom. 
(a)  What is the magnitude of L?
(b)  What are the allowed quantum numbers j, and what is the magnitude of the vector J = L + S?

Solution:

• Concepts:
  Addition of angular momentum
• Reasoning:
  We are supposed to add two orbital and two spinangular momenta  and find the possible values for J.
• Details of the calculation:
  

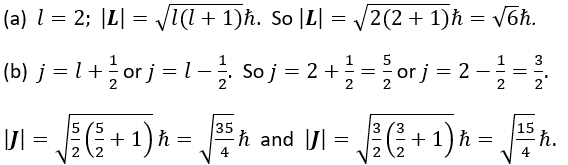
Problem 2:

Studies of the origin of the solar system suggest that sufficiently small particles might be blown out of the solar system by the force of sunlight.  To see how small such particles must be, compare the force of sunlight with the force of gravity, and find the particle radius r at which the two are equal.  Assume that the particles are spherical, act like perfect mirrors, and have a density 2 g/cm³.  
The solar luminosity is L = 3.83*10²⁶ Watts and the solar mass is M_s = 1.99*10³⁰ kg.

Why do you not need to worry about the distance from the Sun?

Solution:

• Concepts:
  Eradiation pressure
• Reasoning:
  We are supposed to recall a basic properties of EM waves.
• Details of the calculation:
  Let k be the unit vector pointing from the sun to the particle.
  Force of gravity:  F_g = -GM_sm/d² k.  Here d is the sun-particle distance.
  m = 4πr³ρ/3 = mass of particle.
  
  Energy of radiation reaching the particle per unit time:  Lπr²/(4πd²) = Lr²/(4d²)
  Assume the particle reflects the radiation like a perfect mirror.  As the radiation reflects, it transfers momentum to the particle. 
  The total momentum transferred is in the k direction and is given by
  p_trans = k 2(p_rad/A) 2πr²∫₀^π/2sinθ cosθ dθ = k 2(p_rad/A) 2πr²∫₀¹x dx = k 2(p_rad/A) πr².
  p_rad/A = L/(4πd²c).  p_trans = k r²L/(2d²c). 
  Momentum transferred to the particle per unit time: Lr²/(2d²c).
  Force of sunlight:  F_s = Lr²/(2d²c) k. 
  
  Equilibrium:  Lr²/(2d²c) = GM_sm/d².  L/(2c) = GM_s4πrρ/3,  r = 3L/(8cGM_sπρ).
  r = 3*3.83*10²⁶/(8*3*10⁸*6.67*10^-11*1.99*10³⁰*π*2000) m = 5.73*10^-5 m.
  Both F_g and F_s decrease proportional to 1/r².

Problem 3:

Consider two particles with angular momenta
J = J₁ + J₂,  J_x = J_1x + J_2x,  J_y = J_1y + J_2y,  J_z = J_1z + J_2z.
J₁ and J₂ are the angular momentum operators of particle 1 and 2, respectively.
Show that the commutators [J²,J₁²] and [J_1z,J²] are zero and nonzero, respectively.  What does it mean in terms of measurements and Heisenberg's uncertainty principle?

Solution:

• Concepts:
  Commutator algebra
• Reasoning:
  We have to add two angular momenta and evaluate two commutators.
• Details of the calculation:
  J₁ and J₂ are angular momentum operators.  For any angular momentum operator we have
  [J_i,J_j] = ε_ijkħJ_k and [J²,J_i] = 0.
  The operator J² = (J₁ + J₂)² may be expressed as J² = J₁² + J₂² + 2J₁∙J₂, since [J₁,J₂] = 0.  J₁ and J₂ operate in different spaces.
  We may write J₁∙J₂ = J_1xJ_2x + J_1yJ_2y + J_1zJ_2z = ½(J₁₊J_2- + J_1-J₂₊ ) + J_1zJ_2z.
  J² commutes with J₁² and J₂².
  [J²,J₁²] = [J₁² + J₂² + 2J₁∙J₂,J₁²] = 0 since [J₁²,J_1i] = 0.
  [J²,J_1z] = [J₁² + J₂² + 2J₁∙J₂,J_1z] = 2[J₁∙J₂,J_1z] = 2[J_1xJ_2x + J_1yJ_2y,J_1z]
  = 2(-J_1yJ_2x + J_1xJ_2y) ≠ 0.
  J² and J₁² are commuting observables and can be measured simultaneously, i.e. the measurement of one does not cause loss of information obtained in the measurement of the other.  After a measurement of J² and J₁² we know their exact values.
  J² and J_1z are non-commuting observables.  They cannot be measured simultaneously, i.e. the measurement of one does cause loss of information obtained in the measurement of the other.  The generalized uncertainty relation states that in any state of the system  
  ΔJ²ΔJ_1z² ≥ ¼|<i[J²,J_1z]>|.

Problem 4:

A plane-polarized electromagnetic wave propagates in free space along the +x axis.
At the position x = 0 the wave encounters a region of infinite extent in the y and z directions which is a low-density plasma of free electrons of number density n, mass m and charge -q_e.  For this plasma region, it is found that the current density j(t) and the electric field  E(t) = E₀exp(-iωt) are related by  j(t) = -nq_ev(t) = -(nq_e²/(imω))E(t).
(a)  Using Maxwell's equations, find the wave number k in the plasma region.  Assume ε = ε₀, μ = μ₀.
(b)  Describe the wave propagation in the plasma region for ω > ω_p and for ω < ω_p, where ω_p² = μ₀nq_e²c²/m = nq_e²/(ε₀m) and specifically determine the depth d of propagation in the plasma for the two cases.
(c)  Is there Joule-heating in the plasma?  If so, compute its value; if not explain why not.

Solution:

• Concepts:
  Newton's 2nd law, charge and current density, plane waves in a conducting medium
• Reasoning:
  We assume that the plasma is neutral overall.  The plasma is a conducting medium.  We can find its conductivity by solving for the motion of the free charges using Newton's second law.  We then derive the wave equation for EM waves in a conducting medium to find the wave number.
• Details of the calculation:
  (a)  Equation of motion for a single charge: md²r/dt² = -q_eE = -q_eE₀exp(i(kx - ωt)).
  r(t) = (q_eE₀/(mω²))exp(i(kx - ωt)).  v(t) = (q_eE₀/(imω))exp(i(kx - ωt)) = (q_e/(imω))E.
  j(t) = -nq_ev(t) = -(nq_e²/(imω))E(t).  j = σE.  σ = (inq_e²/(mω)).
  
  ∇×B = μ₀σE + μ₀ε₀∂E/∂t.
  ∇×(∇×B) = ∇(∇∙B) - ∇²B = μ₀σ(∇×E) + μ₀ε₀∂(∇×E)/∂t.
  ∇²B - μ₀σ∂B/∂t - μ₀ε₀∂²B/∂t² = 0.
  Similarly:  ∇²E - μ₀σ∂E/∂t - μ₀ε₀∂²E/∂t² = 0.
  Note ∇∙E = 0 since E is perpendicular to the direction of propagation.
  Plane wave solutions of the form E = E₀exp(i(kx - ωt)) have to satisfy
  -k² + iωμ₀σ + ω²/c² = 0,  k² = ω²/c² - (μ₀nq_e²/m ) = (1/c²)(ω² - ω_p²),
  k = (1/c)(ω² - ω_p²)^½,
  where ω_p² = μ₀nq_e²c²/m = nq_e²/(ε₀m).
  
  (b)  c/n' = ω/k.  n' = ck/ω = (1 - ω_p²/ω²)^½. 
  For ω_p < ω the index of refraction n' and k are real, the wave propagates freely through the plasma.
  E = E₀exp(i(kx - ωt)).
  For ω_p > ω the index of refraction n' and k are imaginary, the field decreases exponentially.
  E = E₀exp(-αx)exp(-iωt)),  α = |k|.
  Let d be the distance over which the amplitude decreases by a factor 1/e.
  d = 1/α = 1/|k| = c/(ω² - ω_p²)^½.
  
  (c)  dW/dt = ρv∙EdV = j∙EdV = rate at which work is done by the field on the charges in a volume dV.
  j = σE, σ is imaginary, j and E are 90^o out of phase, no Joule heating occurs in the plasma.
  If ω_p < ω, then k is real.  Power enters the plasma and is transported through the plasma by the freely propagating wave.
  If ω_p > ω, then k is imaginary.  The wave does not propagate in the plasma, so it must be completely reflected.

Problem 5:

A sinusoidal electromagnetic wave with angular frequency ω is incident upon an interface at an angle θ with the normal as shown.

Assume ε₂ = ε(ω) is complex, ε(ω) = ε_r + iε_i, μ₁ = μ₂ = μ₀.
Then k_i² = ω²/c²,  k_t² = (ω²/c²)(ε_r + iε_i)/ε₀ = n²ω²/c².
Assume the wave is s-polarized, E = E(t)j.
(a)  Derive an expression for the components of the wave vector k_tx and k_tz in medium 2 when  ε_r = ε_i = ε₀ and θ = 30^o.
(b)  Boundary conditions for the tangential components of E and H yield the ratio E_r/E_i = (cosθ - ncosθ_t)/(cosθ + ncosθ_t).
Write down a complex expression for ncosθ_t and find the fraction of the incident energy absorbed by the medium.

Solution:

• Concepts:
  Maxwell's equations, boundary conditions for the electric and magnetic fields
• Reasoning:
  The tangential component of E is continuous across the boundary.  In the medium k_tx therefore is a real number but k_tz is a complex number.
• Details of the calculation:
  (a)  E_i(r,t) = j E_i exp(i(k_i∙r - ωt)). 
  E_r(r,t) = j E_r exp(i(k_r∙r - ωt)). 
  E_t(r,t) = j E_t exp(i(k_t∙r - ωt)).
  The tangential component of E is continuous across the boundary.  The y-direction is tangential to the interface.  Therefore E_i exp(i(k_i∙r)) + E_r exp(i(k_r∙r)) = E_t exp(i(k_t∙r)) for all r in the z = 0 plane.
  This is only possible if k_i∙r = k_r∙r = k_t∙r for all r in the z = 0 plane.
  Let r = i, then k_ix = k_rx = k_tx = (ω/c)sinθ = 0.5 ω/c.
  k_t² = k_tx² + k_tz²,  k_tz² = (ω²/c²)(ε_r + iε_i)/ε₀ - (ω²/c²)sin²θ.
  k_tz² = (ω²/c²)(ε_r/ε₀ - sin²θ) + i(ω²/c²)ε_i/ε₀.
  k_tz² = (ω²/c²)(0.75 + i).
  k_tz² = |k_tz²|e^iφ,  tanφ = ε_i/(ε_r - ε₀sin²θ),
  |k_tz²| = 1.25(ω²/c²), tanφ = 1/0.75.
  k_tz = |k_tz|e^iφ/2,
  |k_tz| = 1.118 (ω/c)
  k_tz-real = cos(φ/2 )1.118 (ω/c) = ω/c,  k_{tz_im} = 0.5 ω/c.
  k_tx = 0.5 ω/c,  k_tz = (1 + 0.5i)ω/c.
  
  (b)  The index of refraction is a complex number.
  n² = (1 + i).
  ncosθ_t = n(1 - sin²θ_t)^½ = (n² - sin²θ)^½.
  ncosθ_t = (1 + i - sin²θ)^½ = (cos²θ + i)^½ = (0.75 + i)^½
  ncosθ_t = 1.118 e^iφ/2 = 1 + 0.5i.
  Or ncosθ_t = (ck_t/ω)(k_tz/k_t) = 1 + 0.5i.
  |E_r/E_i|² = |(0.866 - 1 - 0.5i)/(0.866 + 1 + 0.5i)|² = 0.0716.
  The intensity that is not reflected is eventually absorbed.
  Fraction absorbed:  1 - 0.716 = 92.84%.