Problems

Problem 1:

A projectile is shot upward from the surface of the Earth at half the escape velocity.  If the escape velocity of the Earth is 11.2 kilometers per second and the radius of the Earth is 6356 km, what is the maximum height reached by the projectile?

Solution:

• Concept:
  Energy conservation
• Reasoning:
  If a projectile with mass m has escape velocity v_e, its total energy is zero, assuming its potential energy is set to zero at infinity.
  E = ½mv_e² - mgR_E = 0,  v_e = (2gR_E)^½. 
• Details of the calculation:
  For an object shot upward with ½v_e,  E = (1/8)mv_e² - mgR_E  = - mgR_E²/R_max.
  (1/8)v_e² - gR_E  = -gR_E²/R_max.   ¼R_E - R_E  = -R_E²/R_max.   R_E/R_max = 3/4. R_max = 4R_E/3 = 8465 km.
  The maximum height reached by the projectile is R_max - R_E = (1/3)R_E = 2119 km above the surface of the Earth.

Problem 2:

Consider a ring of radius R with a circulating current I. 
Using the Biot-Savart law, find the magnetic field B induced by this current along the axis that is perpendicular to the ring and goes through its center.
From the positive side of this axis, the current circulates anticlockwise.

Solution:

• Concept:
  The Biot-Savart law
• Reasoning:
  For filamentary currents we have  B(r) = (μ₀/(4π))∫ I dl'×(r-r')/|r-r'|³.
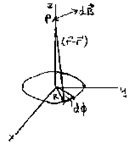• Details of the calculation:
  Choose your coordinate system as shown.
  From the Biot-Savart law we have dB_z(r) = (μ₀/(4π))[I dl'×(r-r')/|r-r'|³] ∙ k.
  On the z-axis r  = zk.
  Symmetry dictates that B = B_zk on the z-axis.
  dl = Rdφ (φ/φ), r - r' = z k - R (ρ/ρ), dl×(r - r') = zRdφ (ρ/ρ) - R²dφ  k.
  dB_z = (μ₀/(4π))[IR²dφ/(R²+z²)^3/2].
  B_z = ∫₀^2πdB_z = ½μ₀IR²/(R² + z²)^3/2.

Problem 3:

For a classroom demonstration, you pass the beam from a HeNe laser (λ = 633 nm) through two identical, closely-spaced slits and observe the interference pattern on a wall 5 m away and perpendicular to the plane containing the slits.   In the darkened classroom, you can clearly observe up to 10 interference maxima on both sides of the central maximum, but the 4^th and 8^th maxima are missing on either side.  The spacing between adjacent maxima on the wall is 1.1 cm.
(a)  What is the spacing between the slits?
(b)  What is the slit width?

Solution:

• Concept:
  Diffraction and interference
• Reasoning:
  Double slit interference can be observed at angles where single slit diffraction provides non-zero intensity.
• Details of the calculation:
  (a)  dsinθ = mλ.  Small angle approximation:  sinθ = tanθ = θ = m*1.1*10^-2/5.
  d = (6.33*10^-7 m)/(2.2*10^-3) = 0.288 mm is the slit separation.
  (b)  The interference maximum at 4*1.1 cm is missing since it falls on the first minimum in the diffraction pattern.  For this first minimum wsinθ = λ,  sinθ = 4.4*10^-2/5.  Therefore w = 71.9 μm is the slit width.

Problem 4:

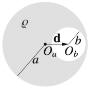A sphere of radius a has uniform charge density ϱ over all its volume, excluding a spherical cavity of radius where b < a where ϱ = 0.  The center of the cavity, O_b, is located at a distance d from the center of the sphere, O_a, with d + b < a. 
Find the electric field inside the cavity.

Solution:

• Concept:
  Gauss' law, the principle of superposition
• Reasoning:
  We can view the sphere with the cavity as a superposition of a sphere with radius a having a uniform charge density ϱ and another sphere with radius b located in the cavity space having a uniform charge density -ϱ.  The field due to each of these spherical charge distributions can be found from Gauss' law.
• Details of the calculation:
  Let the center of the large sphere be located at the origin.
  E = E₁ + E₂.   E₁ = ϱr/3ε₀  for r < R.   E₂ = -ϱ(r - d)/3ε₀  inside the cavity.
  Inside the cavity we therefore have E = ϱr/3ε₀ - ϱr/3ε₀ + ϱd/3ε₀ = ϱd/3ε₀  
  The field inside the cavity is constant and points into the direction of the vector d.

Problem 5:

A man of mass 80 kg achieves ≈ 50 m/s in free fall in the air.  A parachutist with the same mass reaches 5 m/s.  Assume that the air resistance force is proportional to the velocity F = -kv and assume the buoyant force can be neglected.
(a)  What are the values of the k in both of these cases?
(b)  For both cases, what are the distances traveled in t = 10 s if the initial speed is zero?

Solution:

• Concept:
  Newton's second law
• Reasoning:
  F_net = ma is the equation of motion for the object
• Details of the calculation:
  (a)  When the object reaches terminal velocity, its acceleration is a = 0 and the sum of all forces acting on the object is 0.
  0 = mg - kv_t,  k = mg/v_t.
  For the man without parachute:  k = (80 kg)(9.8 m/s²)/(50 m/s) = 15.68 kg/s.
  For the man with parachute:  k = (80 kg)(9.8 m/s²)/(5 m/s) = 156.8 kg/s.

  (b)  a = dv/dt, m(dv/dt) = mg - kv,  dv/dt = g - (k/m)v.
  To a particular solution of the first-order inhomogeneous differential equation we add the solution of the homogeneous differential equation to find the most general solution.
  An inhomogeneous solution:  dv/dt = 0 --> v = v_t .
  Homogeneous solution:  dv/dt = -(k/m)v, v = Cexp(-kt/m), C = constant of integration.
  Most general solution:  v(t) = v_t + Cexp(-kt/m).  v(0) = 0 --> C = -v_t.

  v(t) = v_t - v_texp(-gt/v_t).
  The distance traveled in time t is d =  ∫₀^t(v_t - v_texp(-gt'/v_t))dt' = (v_t)t - (v_t²/g)(1 - exp(-gt/v_t))).
  For the man without parachute:  d = 50*10 - (50²/9.8)(1 - exp(-9.8*10/50)) = 280.83 m.
  For the man with parachute:  d = 5*10 - (5²/9.8)(1 - exp(-9.8*10/5)) = 47.8 m.