More Problems

Problem 1:

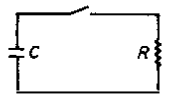
(a)  The capacitor in the circuit in the figure is made from two flat square metal plates of length L on a side and separated by a distance d.  What is the capacitance?
(b)  Show that if any electrical energy is stored in C, it is entirely dissipated in R, after the switch is closed.

Solution:

• Concepts:
  Capacitance, transient RC circuits
• Reasoning:
  As long as R ≠ 0 we ignore the self-inductance of the circuit and we ignore radiation.
• Details of the calculation:
  (a)  For a parallel plate capacitor C = ε₀A/d = ε₀L²/d.
  
  (b)  Let q be the charge on the upper capacitor plate, I the current flowing clockwise after the switch is closed.
  Kirchhoff's loop rule:  q/C - IR = 0.  I = -dq/dt.
  dq/dt + q/(RC) = 0,  q = Q₀e^-t/(RC).  I  = (Q₀/(RC))e^-t/(RC). 
  Energy stored in circuit before the switch is closed:  U = ½Q₀²/C.
  Rate at which the resistor is dissipating electrical energy :  P = I²R = (Q₀²/(RC²))e^-2t/(RC). 
  Total energy dissipated in R:  ΔE = ∫₀^∞Pdt = (Q²₀/(RC²) ∫₀^∞ e^-2t/(RC) dt = ½Q₀²/C = U.
  The electrical energy is stored in C is entirely dissipated in R, after the switch is closed.

Problem 2:

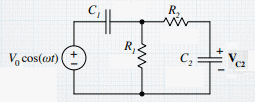
For the AC circuit shown below, find the voltage V_C2 across capacitor C₂ as a function of time.
Let V₀ = 5 V,  ω = 6.667*10⁴/s, R₁ = 3 kΩ, R₂ = 1 kΩ, C₁ = 3*10^-8 F, and C₂ = 1.5*10^-8 F.

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We have a two-terminal network and an AC generator, generating a sinusoidal voltage.
• Details of the calculation:
  Only voltage difference matter.  Choose the node at the bottom of the circuit to be at V = 0.
  There are different approaches to setting up the solution.
  
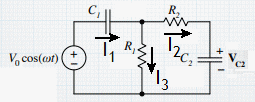
  I₁ = I₂ + I₃. (junction rule)
  V - I₁Z_C1 - I₃R₁ = 0.  (loop rule for left loop)
  I₃R₁ - I₂Z_C2 - I₂R₂ = 0 (loop role for right loop)
  We have 3 equations and 3 ubknowns.
  V_C2 = -I₂Z_C2.
  Eliminate I₁:  V - I₂Z_C1 - I₃Z_C1 - I₃R₁ = 0.
  I₃ = I₂(R₂ + Z_C2 )/R₁.
  Eliminate I₃:  V - I₂Z_C1 - I₂(R₂ + Z_C2 )(Z_C1 + R₁)/R₁ = 0.
  VR₁ - I₂Z_C1R₁ - I₂(R₂ + Z_C2 )(Z_C1 + R₁) = 0.
  I₂ = VR₁/[Z_C1R₁ + (R₂ + Z_C2 )(Z_C1 + R₁)].
  I₂ = VR₁/[-iR₁/(ωC₁) + (R₂ - i/(ωC₂))(-i/(ωC₁) + R₁)].
  I₂ = VR₁/[-iR₁/(ωC₁) - iR₂/(ωC₁) + R₂R₁ - 1/(ω²C₁C₂) - iR₁/(ωC₂)].
  I₂ = VR₁ωC₂/[-iR₁C₂/C₁ - iR₂C₂/C₁ + R₂R₁ωC₂ - 1/(ωC₁) - iR₁].
  V_C2 = -I₂Z_C2  = iI₂/(ωC₂) = V/[C₂/C₁ + (R₂/R₁)(C₂/C₁) + 1 + i(R₂ωC₂ - 1/(ωC₁R₁)].
  Plug in numbers:
  V_C2 = (5 V)/[10/6 + i(0.833] = 2.68V exp(-iφ).
  tanφ = 0.4999,  φ = 0.464 = 26.56^o.
  V_C2 = 2.68V exp(-i 26.56^o).
  
  DIFFERENT APPROACH:
  
  I₁ = I₂ + I₃.   Rewrite in terms of voltages and impedances.
  (V - V_R1)/Z_C1 = (V_R1 - V_C2)/Z_R2 + V_R1/Z_R1,
  (V_R1 - V_C2)/Z_R2 = V_C2/Z_C2.  (Two expressions for I₃.)
  Rearranging:
  [1 + Z_C1/Z_R2 + Z_C1/Z_R1]V_R1 - [Z_C1/Z_R2]V_C2 = V.
  V_R1 = [1 + Z_R2/Z_C2]V_C2.
  Substitute:
  [1 + Z_C1/Z_R2 + Z_C1/Z_R1][1 + Z_R2/Z_C2]V_C2 - [Z_C1/Z_R2]V_C2 = V.
  Plug in the impedances. .
  [1 + 1/(iωR₂C₁) + 1/(iωR₁C₁)][1 + iωR₂C₂]V_C2 - V_C2/(iωR₂C₁) = V.
  Multiply the terms and group the real and imaginary parts.
  V = V_C2[[1 + C₂/C₁ + R₂C₂/(R₁C₁)] + i[ ωR₂C₂ - 1/(ωR₁C₁)]].
  Plug in numbers.
  (1.667 + 0.8333i)V_C2 = 5 V,  1.863 exp(iφ) V_C2 = 5 V
  with tanφ = 0.4999,  φ = 0.464 = 26.56^o.
  V_C2 = 2.68V exp(-i 26.56^o).

Problem 3:

A charged capacitor with C = 590 μF is connected in series to an inductor that has L = 0.330 H and negligible resistance.  At an instant when the current in the inductor is I = 2.50 A, the current is increasing at a rate of dI/dt = 73.0 A/s.  During the current oscillations, what is the maximum voltage across the capacitor?

Solution:

• Concepts:
  LC tank circuit, quasi-static situation
• Reasoning:
  ω = (LC)^-½ = 71.67/s, f = 11.4 Hz, radiation is negligible, energy stored in the circuit is conserved.
  When any closed circuit loop is traversed, the algebraic sum of the changes in the potential must equal zero.
• Details of the calculation:
  Q/C + LdI/dt = 0.  |Q|= LC|dI/dt|.
  U = U_C + U_L = ½Q²/C + ½LI²=  ½L²C |dI/dt|²+ ½LI² = 1.202 J.
  U_Cmax = 1.202 J = ½CV_max².  V_max = 63.8 V.
  or
  Q = Q₀cosωt, I = -ωQ₀sinωt, dI/dt = -ω²Q₀cosωt,  ωI/(dI/dt) = 2.454 = tanωt.
  Q₀ = (dI/dt )/(ω²cosωt) = 3.767*10^-2 C, V_max = Q₀/C = 63.8 V.
  Note:  ωt lies in the third quadrant, the tangent is positive the cosine is negative.

Problem 4:

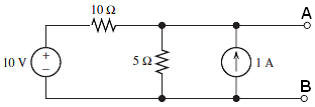
(a)  Find the Thevenin  equivalent circuit for the two terminal circuit shown.
(b)  Find the Norton equivalent circuit for the two terminal circuit shown.

Remember:

• Any two terminal DC network can be replaced by a generator V_Th in series with an resistance R_TH.
• Any two terminal DC network can be replaced by a current source I_N in parallel with an resistance R_N = R_TH.

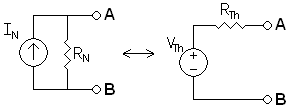
Solution:

• Concepts:
  Equivalent circuits
• Reasoning:
  The Thevenin voltage V_TH is an ideal voltage source equal to the open circuit voltage at the terminals.  The Thevenin resistance R_TH is the resistance measured at the terminals with all voltage sources replaced by short circuits and all current sources replaced by open circuits.
• Details of the calculation:
  (a)  (i)  Find the open circuit voltage.
  Assume point B and the negative terminal of the voltage source are at ground.
  Assume that point A is at voltage V_A.
  Use Kirchhoff's junction rule for the node above the 5 Ω resistor.
  (10 V - V_A)/(10 Ω) + 1 A = V_A/(5 Ω).  V_A = 20/3 V.
  (ii)  Find R_TH.
  1/R_TH = 1/(10 Ω) + 1/(5 Ω).   R_TH = (10/3) Ω.
  (b)  R_N = R_TH =(10/3) Ω.
  I_N is the current flowing through a short circuit.  Since we already determined V_TH and R_TH, we have V_TH - I_NR_TH = 0.
  I_N = V_TH/R_TH = 2A.
  We can also use Kirchhoff's loop rule to find I_N.
  Short out points A and B.  Then no current will flow through the 5 Ω resistor.
  The voltage at point A is zero.
  I_N = (10 V)/(10 Ω) + 1 A = 2 A.
  (Any two of the tree quantities V_TH, R_TH = R_N and I_N determine the third.)