|
Lagrange multipliers, scattering |
|
Addition of angular momentum, EM waves |
|
Producing electromagnetic radiation |
|
Relativistic E&M |
|
Identical particles |
Problem 1:
A bead of mass m is constrained to move without friction on a helix whose equation in
cylindrical polar coordinates is ρ = b, z = aΦ under the influence of
gravity, F = -mg k.
(a)
Use the Lagrange multiplier method and find the appropriate Lagrangian including
terms expressing the constraints.
(b) Apply the Euler-Lagrange
equations to obtain the equations of motion. Solve for the forces of
constraint in the z- and ρ-direction.
(c) If the bead starts from rest at z = 0, find its position as a function
of time.
Solution:
- Concepts:
Lagrangian Mechanics, the Lagrange multiplier method
- Reasoning:
We are instructed to use the Lagrange multiplier method to
solve the problem.
- Details of the calculation:
(a) Lagrangian not incorporating the
constraints:
L = ½m[(dρ/dt)2 + ρ2(dΦ/dt)2 +(dz/dt)2]
- mgz.
Put the equations of constraint into the form
Σk alk
dqk +
alt dt = 0, l = 1, ..., m.
We
have two equations of constraint.
(i) dρ = 0; a1ρ = 1, a1Φ
= a1z = 0.
(ii) dz - adΦ = 0 ; a2ρ = 0, a2Φ
= -a, a2z = 1.
(b) Lagrange's equation:
d/dt(∂L/∂(dqk/dt)) - ∂L/∂qk = ∑lλlalk,
Σk alk dqk + alt dt = 0.
We have:
md2ρ/dt2 - mρ(dΦ/dt)2 = λ1,
mρ2d2Φ/dt2 + 2mρ(dρ/dt)(dΦ/dt) = -aλ2,
md2z/dt2 +
mg = λ2,
and
ρ = b, dρ/dt = d2ρ/dt2 = 0,
z = aΦ, dz/dt = adΦ/dt, d2z/dt2
= ad2Φ/dt2.
We therefore have:
-mb(dΦ/dt)2 = λ1.
mb2 d2Φ/dt2 = -aλ2.
mad2Φ/dt2 +
mg = λ2.
Using
the last two equations to solve for λ2 we have
λ2 = b2mg/(a2 + b2).
Therefore the equation of motion is
d2Φ/dt2 + ag/(a2 + b2) = 0.
d2z/dt2 + a2g/(a2 + b2) = 0.
λ1 = -mb(dΦ/dt)2.
λ1 is the force of
constraint in the radial direction, λ2 is the force of constraint
in the z- direction.
(c) The bead accelerates in the z-direction with
constant acceleration az = -a2g/(a2 + b2).
z(t) = -½azt2, Φ(t) = z(t)/a.
dz/dt = azt. dΦ/dt = azt/a. λ1
= -mb(azt/a)2 = -mb(agt/(a2 + b2))2.
Problem 2:
We study the elastic scattering of two particles m1 and m2 with
interaction energy U(|r1 - r2|) by studying
the scattering of a fictitious particle of reduced mass μ = m1m2/(m1
+ m2) by a potential (energy) U(r). The vector r(r,θ,φ)
describes the relative position of the two particles. It points from particle 2
to particle 1. The vector dr(r,θ,φ)/dt describes the relative
velocity of the two particles, and its direction is the direction of the
velocity of particle 1 in the CM frame. We therefore calculate the cross
section σ(θ,φ) in the CM frame of the two particles. In most experimental
situations, however, particle 1, with velocity v, approaches particle 2,
at rest in the laboratory. We measure the laboratory scattering angles θ0
and φ0 of particle 1. We need the to relate the angles and the cross
sections in the two frames.
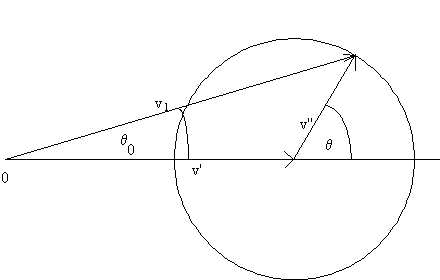
(a) Let v''(θ) be the velocity of particle 1 in the
center of mass frame, v1(θ0)
its velocity in the laboratory frame, and v' the velocity of the center of mass
frame with respect to the laboratory frame.
Derive expressions for the speed v1 and the angle θ0
in terms of m1, m2, v'', and θ.
(b) Derive an expression for the differential scattering cross section σ(θ0,φ0)
in the laboratory frame in terms of σ(θ,φ) in the CM frame, and m1, m2, and
θ.
Solution:
- Concepts:
Frame transformations
- Reasoning:
In the laboratory particle 1 approaches particle 2 with speed v. In the CM
frame particle 1 approaches the CM with speed v'' = m2v/(m1
+ m2) from the left and particle 2 approaches the CM with speed
v' = m1v/(m1
+ m2) from the right. Their relative speed is v and their
total momentum is zero. The speed of the CM in the laboratory is v'.
Using the figure and trigonometry, we can find v1
and θ0
in terms of m1, m2, v'', and θ.
The total number of particles scattered in to a detector is independent of the
reference frame of the observer.
Therefore σ(θ0,φ0)dΩ0 = σ(θ,φ)dΩ.
- Details of the calculation:
(a) v1 = v'' + v'.
v1cosθ0 = v''cosθ + v', v1sinθ0
= v''sinθ, or tanθ0 = sinθ/(cosθ + γ).
Here γ = v'/v'' = m1/m2.
The
ratio v'/v'' is equal to the ratio m1/m2.
θ0 = tan-1(sinθ/(cosθ +
m1/m2)).
v12 = v'2 + v''2
+2v'v''cosθ = (1 + (m1/m2)2)v''2 +
2(m1/m2)v''2cosθ.
(b) σ(θ0,φ0)dΩ0 = σ(θ,φ)dΩ.
σ(θ0,φ0) sinθ0 dθ0 = σ(θ,φ) sinθ dθ.
(The angle φ is the same in the CM and laboratory frame.)
We can therefore write
σ(θ0,φ0) = σ(θ,φ) sinθ dθ/(sinθ0 dθ0)
= σ(θ,φ) dcosθ/dcosθ0.
We have tanθ0 = sinθ/(cosθ + γ). Somehow we have
to use this to evaluate dcosθ/dcosθ0.
Use tanθ0 = (1/cos2θ0 - 1)½ = sinθ/(cosθ + γ).
Let x = cosθ and y = cosθ0.
(1/y2 - 1)½ = (1 - x2)½/(x + γ).
y2 = (x + γ)2/(1 + 2xγ + γ2).
dy/dx = (1 + γx)/(1 + γ2 + 2γx)3/2.
This then yields
σ(θ0,φ0) = σ(θ,φ) (1 + γ2 + 2γcosθ)3/2/|1
+ γcosθ|.
Why absolute value? We can have two different values of x giving the same
value of y. The sign of dy/dx can be a positive or negative sign.
But the solid angle is always a positive number.
We can now compare the cross sections measured in the laboratory frame with the cross
sections calculated in the center of mass frame.
γ = m1/m2.
For γ < 1, m1 < m2,
v' < v'', θ0 increases
monotonically from 0 to π as θ
increases from 0 to π. For γ = 1,
v' = v'', θ0 = ½θ
and varies from 0 to π/2 as θ
varies from 0 to π. No particles appear in the backward
direction. For γ > 1, m1 > m2,
v' > v'', θ0 increases from zero
to a maximum value sin-1(1/γ) as θ
increases from 0 to cos-1(-1/γ). θ0 then decreases to 0 as θ
increases to π. σ0(θ,φ) is usually infinite at the maximum value of θ0.
However this singularity gives a finite
contribution to the total cross section. No particles appear beyond the maximum value of θ0 in the laboratory.
[In the figure the maximum value
of θ0 occurs when v1 is
tangent to the circle.]
Problem 3:
A positive point charge q is moving with constant
velocity v = 103 m/s k along the z axis.
(a) When the charge crosses the origin, find the magnetic field produce by
the point charge at any point (x, y, z) away from the origin as a function of the
Cartesian coordinates x, y, and z.
(b) Express this field on terms of the spherical coordinates (r, θ, φ).
Solution:
- Concepts:
The electromagnetic fields of a moving point charge, the
Lorentz transformation of the electromagnetic fields
- Reasoning:
In the rest frame of the point the electric field is the Coulomb field and
the magnetic field is zero. We can transform those field to a frame in
which the proton is moving with velocity vk.
- Details of the calculation:
(a)
Let K be the rest frame of the point charge. Let the origin of
the two frames coincide at t = 0.
In K,
E = (qe/(4πε0r2))(r/r),
B = 0.
Let K' be the frame in which the point charge is moving with velocity vk.
K' is moving with velocity -vk with respect to K.
In SI units the transformation of the electromagnetic fields to a frame K' moving with velocity
v with respect to the
frame K is given by:
E'|| = E||,
B'|| =
B||, E'⊥
=
γ(E + v×B)⊥,
B'⊥
=
γ(B - (v/c2)×E)⊥.
Here v << c, therefore we can set γ = 1.
Therefore we have
B'|| =
Bz = 0,
B'
=
-(v/c2)×E.
k×E = -Ey i + Ex j.
Ey = (qe/(4πε0))(y/(z2
+ x2 + y2)3/2.
Ex = (qe/(4πε0))(x/(z2
+ x2 + y2)3/2.
B'
=
-(v/c2)Ey i + (v/c2)Ex
j
= (v/c2)(qe/(4πε0))[-(y/(z2
+ x2 + y2)3/2) i + (x/(z2
+ x2 + y2)3/2) j]
Since v << c, (x' y', z') = (x, y, z).
(b) Transforming to spherical coordinates:
z2
+ x2 + y2 = r2.
B' = (v/c2)(qe/(4πε0r3))(-y
i + x j)
= (v/c2)(qesinθ/(4πε0r2))
eφ
= (μ0/(4πr2))qev sinθ eφ
= (μ0/(4πr2))qev×er.
Problem 4:
Consider three (non-interacting) particles in thermal equilibrium, in a
one-dimensional harmonic oscillator, with a total energy E = (7/2)ћω.
(Reminder: the energies of the one-particle states are En = ½ћω + nћω, with
n = 0, 1, 2, ..., ).
(a) If they are distinguishable particles (all with the same ω), what are the
possible occupation-number configurations, and how many distinct (three
particle) states are there for each one? If you picked a particle at
random and measured the energy, what values might you get, and what is the
probability of each one? Check that the sum of probabilities is 1.
(b) Repeat for identical fermions, ignoring spin.
(c) Repeat for identical bosons, also ignoring spin.
Solution:
- Concepts:
Identical particles
- Reasoning:
Fermions, bosons and classical particles obey different probability laws.
- Details of the calculation:
(a) E = (3/2)ћω + ћω(n1 + n2 + n3) =
(7/2)ћω.
n1 + n2 + n3 = 2. Therefore the
particles can only occupy states with n = 0, 1, and 2.
Since the particles are distinguishable, we can give them unique labels.
| State |
particle |
particle |
particle |
particle |
particle |
particle |
| n = 2 |
3 |
2 |
1 |
|
|
|
| n = 1 |
|
|
|
2, 3 |
1, 3 |
1, 2 |
| n = 0 |
1, 2 |
1, 3 |
2, 3 |
1 |
2 |
3 |
There are 6 distinct 3-particle states with energy (7/2)ћω.
If a particle is picked at random, it is equally likely to be any of the 3
particles in any of the 6 states. There are 18 distinct possibilities.
9/18 = ½ of the time it will have energy E = ½ћω.
6/18 = 1/3 of the time it will have energy E = (3/2)ћω.
3/18 = 1/6 of the time it will have energy E = (5/2)ћω.
P(n = 0) + P(n = 1) + P(n = 2) = ½ + 1/3 + 1/6 = 1.
(b) For identical fermions (excluding spin) there are no states
with E = (7/2)ћω, since the Pauli exclusion principle does not allow two
identical fermions to have exactly the same quantum numbers.
(c) For identical bosons, we construct the following table.
| State |
particle |
particle |
| n = 2 |
b |
|
| n = 1 |
|
b, b |
| n = 0 |
b, b |
b |
(We label the particles with the same symbol b, since they are
indistinguishable.)
There are 2 distinct 3-particle states with energy (7/2)ћω.
If a particle is picked at random, it is equally likely to be any of the 3
particles in any of the 2 states.
3/6 of the time it will have energy E = ½ћω.
2/6 of the time it will have energy E = (3/2)ћω.
1/6 of the time it will have energy E = (5/2)ћω.
P(n = 0) + P(n = 1) + P(n = 2) = ½ + 1/3 + 1/6 = 1.

