More Problems

Problem 1:

A capacitor composed of two parallel infinite conducting sheets separated by a distance d is connected to a battery.  The lower plate is maintained at some potential V₁ and the upper plate is maintained at some potential V.  A small hemispherical boss of radius a << d is introduced on the lower plate.  State the boundary conditions for this problem.  (Hint: Consider the limit as the distance between the plates becomes very large.)  Find the potential between the plates and the surface charge density on the plates.

Solution:

• Concepts:
  Boundary value problems, azimuthal symmetry.
• Reasoning:
  Put the origin of the coordinate system at the center of a sphere, the upper half of which is the hemispherical boss.  Let the z-axis point up.
  Then Φ(r,θ) = ∑_n=0^∞[A_nrⁿ + B_n/rⁿ⁺¹]P_n(cosθ) is the most general solution in the region between the plates, since the charge density ρ = 0 there.  To find the specific solution we apply boundary conditions.
• Details of the calculation:
  The boundary conditions are Φ = V₁ on the lower plate and the boss and Φ = V on the upper plate.
  Φ = V₁ + A₁'rcosθ  + (B₁'/r²)cosθ  between the plates outside the boss.
  We assume all other coefficients are zero.  If we find a solution with this assumption, it is the only solution.
  Boundary conditions:
  (i)  Φ is continuous at r = a.  0 = A₁'a + B₁'/a².  B₁' = -A₁'a³.
  (ii)  E = -∇Φ = E₀ at r >> a,  i.e. far away from the hemispherical boss.
  -A₁'cosθ = E₀cosθ,  A₁'sinθ = -E₀sinθ,  A₁' = -E₀,  B₁' = E₀a³.  E₀ = (V - V₁)/d.
  Therefore
  Φ = V₁ - E₀rcosθ  + (E₀a³/r²)cosθ.
  E_r = E₀cosθ  + 2(E₀a³/r³)cosθ,  E_θ = -E₀sinθ + (E₀a³/r³)sinθ.
  E = E₀ + 2(E₀a³/r³)cosθ (r/r) + (E₀a³/r³)sinθ (θ/θ).
  E = external field + field due to polarized sphere.
  
  Surface charge on the plates: σ = ε₀E·n.
  E·n = -E₀ on the upper plate, σ = -ε₀E₀.
  E·n = -E_θ = E₀ - (E₀a³/r³) on the flat part of the lower plate, σ = ε₀E₀ - ε₀(E₀a³/r³).
  E·n = E_r = 3E₀cosθ on the boss, σ = ε₀3E₀cosθ.

Problem 2

A charge q is located in the empty space above an infinite, flat, grounded conducting plate whose surface coincides with the plane at z = 0.
The coordinates of the charge are (x, y, z) = (0, 0, d) with d > 0.
(a)  Calculate the force acting on the charge.
(b)  Calculate the electric field in the half-space z > 0.
(c)  What is the surface charge density induced on the surface of the plate?
(d)  How much work would be needed to pull the charge q away to z = +∞ along the z-axis?

Solution:

• Concepts:
  The method of images
• Reasoning:
  This problem involves a point charge in front of a conducting plane.  The method of images yields the potential energy of the point charge and the force on the point charge.
• Details of the calculation:
  If the charge is a distance d from the conducting plane, it is a distance 2d from its image.
  (a)  The force on the charge is F_z = -q²/(16πε₀d²).
  
  (b)  E(x,y,z) = [q/(4πε₀)](xi + yj + (z - d)k)/(x² + y² + (z - d)²)^3/2
  - [q/(4πε₀)](xi + yj + (z + d)k)/(x² + y² + (z + d)²)^3/2.
  
  (c)  E(x,y,0) = [q/(4πε₀)](xi + yj - dk)/(x² + y² + d²)^3/2
  - [q/(4πε₀)](xi + yj + dk)/(x² + y² + d)^3/2.
  E(x,y,0) = -[qdk/(2πε₀)]/(x² + y² + d²)^3/2.
  Surface charge density σ(x,y) = ε₀E(x,y,0)·n = -[qd/(2π)]/(x² + y² + d²)^3/2.
  σ(ρ) = -[qd/(2π)]/(ρ² + d²)^3/2.
  
  (d)  The potential energy of the point charge (the negative of the work necessary to remove the charge from its position to infinity) is U  = -q²/(16πε₀d).
  W = q²/(16πε₀)∫_d^∞dz/z² = q²/(16πε₀d) is the work needed to pull the charge q away to z = +∞.

Problem 3:

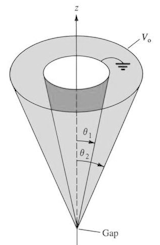Two conducting cones (0 < θ₁ <  θ₂ < π/2) of infinite extend are separated by an infinitesimal gap at r = 0.  Let V(θ₁) = 0 and V(θ₂) = V₀.  Find V between the cones.

Laplacian in spherical coordinates: 


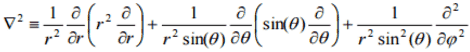
∫dx/sinx = ln(tan(x/2))

Solution:

• Concepts:
  Laplace's equation in spherical coordinates
• Reasoning:
  Since the cones are infinite, V can only depend on θ.
  (Rotational symmetry  --> no φ dependence
  System is unchanged if we change the scale  --> no r dependence)
  ∇²V = 0  becomes
  (1/(r²sinθ))∂/∂θ(sinθ ∂V/∂θ) = 0.
  Since r = 0 is excluded due to the insulating gap, we can write ∂/∂θ(sinθ ∂V/∂θ) = 0.
• Details of the calculation:
  Integrating once gives sinθ ∂V/∂θ = A, or ∂V/∂θ = A/sinθ.
  Integrating again gives V = A ln(tan(θ/2)) + B.
  Boundary conditions:
  V(θ₁) = 0 --> B = -A ln(tan(θ₁/2)).
  V(θ₂) = V₀ --> A ln(tan(θ₂/2))  - A ln(tan(θ₁/2)) = A ln[tan(θ₂/2)/tan(θ₁/2)] = V₀.
  A = V₀/ln[tan(θ₂/2)/tan(θ₁/2)].
  V(θ)  = A ln[tan(θ/2)/tan(θ₁/2)] = V₀ ln[tan(θ/2)/tan(θ₁/2)]/ln[tan(θ₂/2)/tan(θ₁/2)].