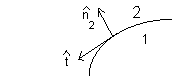Electrostatics

The fundamental equations of electrostatics are linear equations,
∇·E = ρ/ε₀,  ∇×E = 0, (SI units).
The principle of superposition holds.

The electrostatic force on a particle with charge q at position r is F = qE(r).
∇×E = 0 <==> E = -∇Φ,  ∇²Φ = -ρ/ε₀.
Φ is the electrostatic potential.

Dipoles

The field of a dipole at the origin:  E(r) = [1/(4πε₀)](1/r³)[3(p·r)r/r² - p].
The potential of a dipole at the origin:  Φ(r) = [1/(4πε₀)](p·r)/r³.
The force on a dipole:  F = ∇(p·E).
The torque on a dipole:  τ = p×E.
The energy of a dipole in an external field:  U = -p·E.

Properties of conductors in electrostatics

• E = 0 inside.
• ρ = 0 inside.
• Any excess charge resides on the surface.
• E on the surface is perpendicular to the surface.
• E = (σ/ε₀)n just outside the surface.

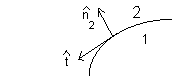Boundary conditions in electrostatics

(E₂ - E₁)·n₂ = (σ/ε₀),
(E₂ - E₁)·t = 0,
(D₂ - D₁)·n₂ = σ_f,
Φ is continuous across the boundary.

Methods for solving electrostatic problems

The multipole expansion

For a charge distribution located near the origin we have
Φ(r) = [1/(4πε₀)][(1/r)[∫_v' dV' ρ(r') + (1/r² )(r/r)·[∫_v' dV' ρ(r')r'
+ (1/r³ )[∫_v' dV'ρ(r')(3(r·r')²/r² - r'²)/2 + ... ]
= 1/(4πε₀)][Q/r) + p·(r/r)/r² + (1/(2r⁵))∑_ij3x_ix_jQ_ij + ... ],
with p = ∫_v' dV' ρ(r')r' and
Q_ij = ∫(x_i'x_j' - (1/3)δ_ijr'²) ρ(r')dV',  Q_ij = Q_ji,  ∑_iQ_ii = 0.

Here Q = total charge, p = dipole moment, Q_ij = quadrupole moment tensor of the charge distribution.  If the problem has rotational symmetry about the z-axis, such that Q_xx = Q_yy = -½Q_zz, then Q_zz is called the quadrupole moment.

The energy of a charge distribution near the origin in an external field is given by
W = qΦ(0) - p·E(0) - ½∑_i∑_jQ_ij ∂E_j/∂x_i|_xi=0 + ... .
This expansion shows how the various multipoles interact with the external field.

The method of images

Consider a charge q at z = d on the z - axis.

• Assume the z = 0 plane is a grounded conducting plane.  Then placing an image charge q' = -q at  d' = -d on the z-axis makes the z = 0 plane an equipotential with Φ = 0.
• Assume a grounded conducting sphere of radius R < d is centered on the origin.  Then placing an image charge q' = -qR/d at d' = R²/d on the z-axis makes the sphere an equipotential with Φ = 0.  Add q'' at the center of the sphere to change the potential or the total charge on the sphere.

Consider a line charge λ parallel to the x-axis at d = d k.

• Assume a conducting cylinder of radius R < d has as its symmetry axis the x-axis.  Then placing an image line charge λ' = -λ at d' k with d' = R²/d parallel to the x-axis makes the cylinder an equipotential with Φ = [λ/(2πε₀)]ln(R/d).  Add V₀ everywhere to change the potential of the cylinder.

The method of images with dielectrics

Assume the z = 0 plane is a plane interface between two dielectrics. 
Consider a charge q at z = d on the z-axis in ε₁.  Then placing an image charge q' = -q(ε₂ - ε₁)/(ε₂ + ε₁) at z' = -d on the z-axis in a medium with ε₁ gives the potential and field in dielectric 1.  And replacing q with an image q'' = q(2ε₂)/(ε₂ + ε₁) charge at z''= d  on the z-axis in a medium with ε₂ gives the potential and field in dielectric 2.

The uniqueness theorem

When solving electrostatic problems, we often rely on the uniqueness theorem.  If the charge density ρ is specified throughout a volume V, and Φ or its normal derivatives are specified at the boundaries of a volume V, then a unique solution exists for Φ inside V.

Boundary value problems

In regions with ρ = 0 we have ∇²Φ = 0.  We are looking for a solution for ∇²Φ = 0, subject to boundary conditions.
Let Φ =  Φ(r,θ),  0 ≤ θ ≤ π  in spherical coordinates, i.e. let the problem have azimuthal symmetry.
Then the most general solution for ∇²Φ = 0 is
Φ(r,θ) = ∑_n=0^∞[A_nrⁿ + B_n/rⁿ⁺¹]P_n(cosθ).

Let Φ =  Φ(ρ,φ),  0 ≤ θ ≤ 2π  in cylindrical coordinates.
Then the most general solution for ∇²Φ = 0 is
Φ(ρ,φ) = ∑_n=1^∞(A_ncos(nφ) +  B_nsin(nφ))ρⁿ + ∑_n=1^∞(A'_ncos(nφ) +  B'_nsin(nφ))ρ^-n + a₀ + b₀lnρ.