More Problems

Problem 1:

Consider the magnetic vector potentials A₁ = (-By, 0, 0) and A₂ = -½(By, -Bx, 0).
(a)  Show that both vector potentials are associated with the same magnetic field B.
(b)  Construct a gauge transformation ψ(r) which connects the two representations of the vector potential.

Solution:

• Concepts:
  ∇∙B = 0 --> B = ∇×A.
• Reasoning:
  A is not unique.  A' = A + ∇ψ + C, with ψ an arbitrary scalar field and C an arbitrary constant vector is also a vector potential for the same field.  In magnetostatics we choose ∇∙A = 0.
• Details of the calculation:
  (a)  ∇×A = (∂A_z/∂y - ∂A_y/∂z,  ∂A_x/∂z  -  ∂A_z/∂x,  ∂A_y/∂x -  ∂A_x/∂y).
  ∇×A₁ = -(∂A_x/∂y) k = B k.
  ∇×A₂ = (∂A_y/∂x -  ∂A_x/∂y) k = B k.
  (b)  A₂ - A₁ = ∇ψ = ½(By, Bx, 0),  ψ = ½Byx.

Problem 2:

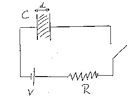A parallel-plate capacitor consists of two circular metal plates of radius a, separated by a distance d.  The insulating material between the plates has a dielectric permittivity ε.  The capacitor is part of the circuit shown.
At time t = 0 we close the switch.  As a function of time, and ignoring edge effects, compute the following quantities for all spatial points within the dielectric material:
(i)  the electric field,
(ii)  the magnetic field,
(iii)  the Poynting vector,
(iv)  the energy density.
Finally, (v) give the total energy stored in the capacitor as t --> ∞.  Check that it is equal to the field energy that has been flowing into the capacitor.

Express your answers to (i) - (v) in terms of the circuit elements C, R, and V.

Solution:

• Concepts:
  Transient fields, the Poynting vector
• Reasoning:
  We are asked to solve for the transients in a circuit and comment on the energy density and the energy flux.
• Details of the calculation:
  For a parallel plate capacitor we have  C = εA/d.  Here A = πa²,  C = επa²/d.
  When the switch is closed we have from Kirchhoff's loop rule V - IR - Q/C = 0.
  Dividing by R we have
  dQ/dt + Q/(RC) - V/R = 0.  Try a solution of the form Q = A(1 - e^-λt).
  Aλe^-λt + A/(RC) - Ae^-λt/(RC) - V/R = 0 for all t.
  This implies A/(RC) = V/R, A = VC and Aλ = A/(RC), λ = 1/(RC).
  Q = VC(1 - e^-t/(RC)).
  The voltage across the capacitor as a function of time is Q/C, and in the dielectric we have
  E = k Q/(dC) as a function of time.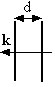
  (i)  E = (V/d)( 1- e^-t/(RC)) k.
  (ii)  ∇×B = μ₀ε∂E/∂t,  B = B (φ/φ),  2πrB = πr²μ₀ε∂E/∂t,  B = [μ₀εrV/(2dRC)]e^-t/(RC).
  (iii)  S = (1/μ₀)(E×B).
  S = -(V/d)(1-e^-t/(RC))[εrV/(2dRC)]e^-t/(RC)(ρ/ρ) = -[εrV²/(2d²RC)](1-e^-t/(RC))e^-t/(RC) (ρ/ρ).
  Field energy is flowing into the capacitor from the sides.
  (iv)  u = (1/2μ₀)B² + (ε/2)E² = μ₀[εrV/(dRC)]²e^-2t/(RC)/8 + ε(V/d)²(1-e^-t/(RC))²/2.
  (v)  As t --> ∞  u = ε(V/d)²/2,  U = πa²εV²/(2d) = CV²/2 = total energy stored in the capacitor.
  Check:  ∫₀^∞dt S(a)2π ad = (V²/R)∫₀^∞dt[e^-t/(RC) - e^-2t/(RC)] = V²C - ½V²C = ½V²C.

Problem 3:

The Aharanov-Bohm experiment is illustrated in the figure below.

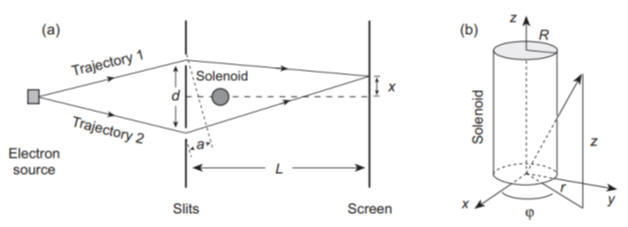
It is a two-slit electron scattering experiment where a solenoid is placed in the region behind the screen and between the two classical paths that electrons passing through the slits would follow to reach a point on the screen.  The long and thin solenoid confines the magnetic field to regions that the electrons should not pass through.  In terms of the cylindrical coordinates in Fig (b), the magnetic field may be assumed given by

inside solenoid:              B_r = 0,  B_φ = 0,  B_z = B.
outside solenoid:            B_r = 0,  B_φ = 0,  B_z = 0.

(a)  Show that a vector potential given in the cylindrical coordinates by
inside the solenoid:        A_r = A_z = 0,   A_φ = Br/2.
outside the solenoid:     A_r = A_z = 0,  A = BR²/(2r),
leads to the magnetic field components inside and outside the solenoid given above.

Thus, in the Aharanov-Bohm experiment the electrons never experience a finite magnetic field but they may encounter a non-zero vector potential outside the solenoid.

(b)  What does this result, and that in the Aharanov-Bohm experiment the interference pattern is observed to be shifted when current is flowing in the solenoid, say about the relative importance of the magnetic field and the vector potential in classical and quantum mechanics?

Solution:

• Concepts:
  ∇∙B = 0 --> B = ∇×A.
• Reasoning:
  We can evaluate ∇×A in Cartesian or cylindrical coordinates.
• Details of the calculation:
  (a)  In Cartesian coordinates:
  A_x = -A_φsinφ,  A_y = A_φcosφ,  A_z = 0.
  B = ∇×A = (∂A_z/∂y - ∂A_y/∂z,  ∂A_x/∂z  -  ∂A_z/∂x,  ∂A_y/∂x -  ∂A_x/∂y).
  
  Inside:  A_x = -½Br(y/r) = -½By,  A_y = ½Bx,  A_z = 0.
  B = (0, 0, B_z),  B_z = ∂A_y/∂x - ∂A_x/∂y = ½B + ½B = B.
  Outside: A_x = -½BR²y/(x² + y²),  A_y = ½BR²x/(x² + y²),    A_z = 0.
  B = (0, 0, B_z),  B_z = ∂A_y/∂x -  ∂A_x/∂y = ½BR²(1/r² - 2x²/r⁴ + 1/r² - 2y²/r⁴)
  = ½BR²(2/r² - 2/r²) = 0.
  [In cylindrical coordinates we use
  B_z = (∂(rA_φ)/∂r - ∂A_r/∂φ)/r,  B_r = (∂A_z/∂φ - r∂A_φ/∂z)/r,  B_φ = ∂A_r/∂z - ∂A_z/∂r,
  to obtain the same result.]
  
  (b) In classical mechanics electrons would be acted on by the Lorentz force, which requires a finite magnetic field, and the vector potential has no effect except through the magnetic field.  But in quantum mechanics the Aharonov-Bohm experiment shows that the vector potential can cause physical effects even if the corresponding magnetic field vanishes.