Review
Problem 1:
A neutral Na atom has eleven electrons. Ten electrons are removed to form a Na10+ ion. Calculate the frequency in Hz and the wavelength in nm of the n = 2 to n = 1 transition of the Na10+ ion.
Solution:
- Concepts:
Hydrogenic atoms, scaling rules - Reasoning:
Na10+ is a single electron ion, the nuclear charge is Z = 11. - Details of the calculation:
En = -13.6 eV (μ'/μ)Z2/n2 = -13.6 eV*121/n2.
E2 - E1 = 121*(-3.4 + 13.6) eV = 1234.2 eV = hf = (4.136*10-15 eV s)*f. f = 2.98*1017/s.
λ = c/f = 1.01 nm.
Problem 2:
Assume a uniform electric field E = Ek exists in some region of
space that contains no magnetic field. Let the magnetic vector potential
A(r,t) be zero. Write down an electrostatic potential Φ(r,t) for this field.
Define a gauge transformation, so that Φ'(r,t) = 0. What is the corresponding
vector potential A'?
Solution:
- Concepts:
Gauge transformations - Reasoning:
A and Φ are not unique. - Details of the calculation:
Φ(r,t) = -Ez is a possible electrostatic potential for this field.
Φ' = Φ - ∂λ/∂t = 0. λ = -Ezt.
A' = ∇λ = -Etk.
Problem 3:
We connect a real inductor to a source of alternating voltage with an amplitude of 10 V and a frequency of 60 Hz. A current with an amplitude of 16 mA flows through this circuit. The amplitude of the current drops to 12 mA when we connect a resistor with a resistance of 500 Ω in series with the inductor. Find the inductance L and the resistance RL of the inductor.
Solution:
- Concepts:
AC circuits - Reasoning:
A real inductor has some resistance. We model it as an ideal inductor L in series with a resistor RL.
For any series RL circuit we have Z = R + iωL, |Z| = (R2 + ω2L2)½, |I| = |V|/|Z|. - Details of the calculation:
1.6*10-2 A = 10/(RL2 + ω2L2)½, 1.2*10-2 A = 10/((RL + 500 Ω)2 + ω2L2)½.
We have 2 equations for two unknowns.
In SI units:
RL2 + ω2L2 = (10/1.6*10-2)2 = 6252. ω2L2 = 6252 - RL2.
(RL + 500)2 + 6252 - RL2 = 1000 RL + 5002 + 6252 = 8332.
RL = 53.8 Ω.
ωL = 623 H/s, L = 1.65 H.
Problem 4:
Consider a two-state system. The eigenbasis of the Hamiltonian H0 is {|1>, |2>}, and in that basis the matrix of the H0 is
H0 = ħ
| ω0 | 0 | ||
| 0 | ω0 |
.
Let H = H0 + W be the Hamiltonian of the system when a small perturbation is applied, and let the matrix of W in the {|1>, |2>} basis be
W = ħ
| 0 | ε1 | ||
| ε2 | 0 |
.
Find the eigenvalues of H to first order using stationary perturbation theory, and find the corresponding zeroth order normalized eigenstates.
Solution:
- Concepts:
First order perturbation theory for degenerate states - Reasoning:
We have to diagonalize the matrix of W in the subspace of degenerate states. - Details of the calculation:
(a) det(W - λI) = 0 yields λ2 - ħ2ε1ε2 = 0.
λ± = ± ħ(ε1ε2)½ are the first-order corrections.
To first order the eigenvalues of H are
E+ = ħ(ω0 + (ε1ε2)½) and E- = ħ(ω0 - (ε1ε2)½).
The corresponding eigenstates are
|ψ+> = N(|1> + (ε2/ε2)½|2>)
and
|ψ-> = (|1> - (ε2/ε2)½|2>),
with N = (ε1/(ε1 + ε2))½.
Problem 5:
A rectangular trough extends infinitely along the z direction, and has a cross section as shown in the figure.
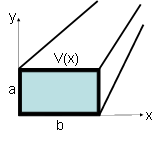
All the faces are grounded, except for the top one, which is held at a potential V(x) = V0. Find the potential inside the trough.
Solution:
- Concepts:
General solution to Laplace's equation, boundary conditions - Reasoning:
ρ = 0 inside the trough, ∇2V = 0 inside the trough. - Details of the calculation:
This is a two-dimensional problem. V does not depend on z.
In Cartesian coordinates ∇2V = ∂2V/∂x2 + ∂2V/∂y2 = 0.
Separation of variables: V(x,y) = F1(x)F2(y).
(1/F1)∂2F1/∂x2 + (1/F2)∂2F2/∂y2 = 0.
Since each term in the sum is a function of a different independent variable, each term must be equal to a constant and the constants have to sum to zero.
Let (1/F1)∂2F1/∂x2 = -C2, ∂2F1/∂x2 + C2F1 = 0.
Then (1/F2)∂2F2/∂y2 = C2, ∂2F2/∂y2 - C2F2 = 0.
Solutions that can fulfill the boundary conditions on all faces with V = 0 require
F1(x) = sin(Cx), C = nπ/b, F2(y) = sinh(Cy), n = 1, 2, 3, ... .
The solution that satisfies all boundary conditions is
V(x,y) = ∑n=1∞Dn sin(nπx/b) sinh(nπy/b),
subject to the boundary condition V(x,a) = V0.
V0 = ∑n=1∞Dn sin(nπx/b) sinh(nπa/b).
Property of the sine functions:
∫0bdx V0sin(pπx/b) = 2V0b/(pπ) if p is odd, 0 otherwise.
But ∫0bdx V0sin(pπx/b) = ∑n=1∞ Dn sinh(nπa/b) ∫0bdx sin(pπx/b) sin(nπx/b) = Dp sinh(pπa/b)(b/2).
Therefore Dp = 4V0/(pπ sinh(pπa/b)), p = odd, 0 otherwise.
Problem: 5
A very large sheet of electric charge densities +σ lies parallel to and a small distance d1 in front of a very large grounded conducting plane. A point charge +q is placed a distance d2 < d1 in front of the plane, very far from the edges. The plane and the sheet are held in place. Find the external force required to also keep the point charge at rest.
Solution:
- Concepts:
Gauss' law. method of images, - Reasoning:
This problem involves charge distributions in front of a conducting plane. - Details of the calculation:
Locate the grounded conducting plane at z = 0, the sheet at z = d1, and put the point charge at on the z-axis at z = d2.
The positively charged sheet induces a surface charge, which produces an electric field equal to that produced by an image sheet of charge densities -σ at a distance z = -d1. The point charge +q also induces a surface charge distribution, which produces an electric field equal to that produced by an image charge -q on the z-axis at z = -d2. The electric force acting on q is a superposition of the forces due to the sheet, the image sheet and the image charge.
The field due to an very large charged surface near the surface is found from Gauss' law.
On the z-axis, in the region 0 < z < d1 the field due to all charges except q itself is
E = E(+σ) + E(-σ) + E(q) = k[-σ/(2ε0) - σ/(2ε0) - q/(4πε0(z + d2)2)].
Electric force on q: Fel = qE = -k[ qσ/ε0 + q2/(16πε0d22)].
External force required to also keep the point charge at rest: Fext = -Fel.