Time-dependent perturbation theory

Let H = H₀ + W(t). 
Let {|Φ_p>} be an orthonormal eigenbasis of H₀,  H₀|Φ_p> = E_p|Φ_p>.
Let  ω_fi = (E_f - E_i)/ħ and W_fi(t) = <Φ_f|W(t)|Φ_i>.
Assume that at t = 0 the system is in the state |Φ_i>.
The probability of finding the system in the state |Φ_f> (f ≠ i) at time t is
P_if(t) = (1/ħ²)|∫₀^texp(iω_fit')W_fi(t')dt'|²,
in first order time-dependent perturbation theory.  (Derivation)

Fermi's golden rule

Assume there exists a group of states nearly equal in energy  E = E_i + ħω.
Let ρ(β,E) be the density of final states, i.e. ρ(β,E)dE is the number of final states in the interval dE characterized by some discrete index β. 
Let W(t) = Wexp(±iωt).  Then the transition probability per unit time is given by
w(i,βE) = (2π/ħ)ρ(β,E)|W_Ei|²δ_E-Ei,ħω, where W_Ei = <Φ_E|W|Φ_i>.
This is Fermi's golden rule.
The transition probability increases linearly with time.

Details:
Assume there is a group of states n, nearly equal in energy E, and that W_ni = <Φ_n|W(t)|Φ_i> is nearly independent of n for these states.  Take for example continuum states.  We may label continuum states by |α>, where α is continuous and <α|α'> = δ(α - α'). 
The probability of making a transition to one of these states in a small range Δα is ∫_Δα|<α|Ψ(t)>|²dα.
If |α> = |β,E> then dα = ρ(β,E)dE, where ρ(β,E) is the density of states. 
We assume β to be some discrete index.  We then have
δP(i,βE) = ∫_ΔE ρ(β,E)|<βE|Ψ(t)>|²dE.
If W is a constant perturbation, then δP(i,βE) = ∫_ΔE dE ρ(β,E)[|W_Ei|²/ħ²] sin²(ω_Eit/2)/(ω_Ei/2)².
The function sin²(ω_Eit/2)/(ω_Ei/2)² peaks at ω_Ei = 0 and has an appreciable amplitude only in a small interval Δω_Ei or ΔE about ω_Ei = 0.  We assume that ρ(β,E) and |W_Ei|² are nearly constant in that small interval and therefore may be taken out of the integral.  Then
δP(i,βE) = ρ(β,E)[|W_Ei|²/ħ²]∫ dħω_Ei sin²(ω_Eit/2)/(ω_Ei/2)²
= ρ(β,E)[|W_Ei|²/ħ²]2ħ ∫dx sin²(xt)/x².
∫_-∞^∞dy sin²(y)/y² = π.
We have (πt)^-1∫dx sin²(xt)/x² = 1.  Therefore
δP(i,βE) = (2π/ħ) ρ(β,E) |W_Ei|² δ(E - E_i)t.
(It is understood that this expression is integrated with respect to dE.)
The transition probability per unit time is the given by Fermi's golden rule,
w(i,βE) = (2π/ħ) ρ(β,E) |W_Ei|² δ(E - E_i).
Similarly, for a sinusoidal perturbation W(t) = Wsinωt or W(t) = Wcosωt we obtain
w(i,βE) = (π/2ħ) ρ(β,E) |W_Ei|² δ(E - E_i - ħω).
and for W(t) = Wexp(±iωt) we obtain w(i,βE) = (2π/ħ) ρ(β,E) |W_Ei|² δ(E - E_i - ħω).

Dipole transition selection rules

When an atom interacts with an electromagnetic wave, the electromagnetic field is most likely to induce a transition between an initial and a final atomic state if these selection rules are satisfied.  If these selection rules are not satisfied a transition is less likely and is said to be forbidden.
The selection rules are:
If H₀ = p²/2m + U(r), i.e. if we are neglecting the spin-orbit coupling,
Δl = ±1, Δm = 0, ±1.
If H₀ contains a spin orbit coupling term f(r)L∙S, then the dipole selection rules then become
Δj = 0, ±1, (except j_i = j_f = 0), Δl = ±1, Δm_j = 0, ±1.

Elastic scattering

In a typical scattering experiment a target is struck by a beam of mono-energetic particles.
Let F_i be the incident flux, i.e. the number of particles per unit area per unit time. 
F_i = n_pv, where n_p is the number of particles per unit volume. 
Typically n_p is very small and we can neglect any interaction between different incident particles.
We measure the number ΔN_p of particles scattered per unit time into a solid angle ΔΩ about the direction defined by the spherical coordinates θ and φ. 
We expect ΔN_p ∝ F_i, and ΔN_p ∝ ΔΩ .
We define ΔN_p = σ_t(θ,φ)F_iΔΩ.  Here σ_t(θ,φ) is the differential scattering cross section of the target.  It has the units of an area.  Commonly used units are cm² and barn = 10^-24 cm².

The Born approximation

The elastic scattering cross section in the Born Approximation is
σ_k^B(θ,φ) = σ_k^B(k,k') = [μ²/(4п²ħ⁴)]|∫d³r' exp(-iq∙r')U(r')|²,
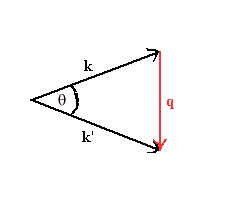
where q = k' - k, k = μv₀/ħ, k' = μv₀/ħ (k'/k'), and μ is the reduced mass.

The differential scattering cross section is proportional to the square of the Fourier transform of the potential.
We often want to know the scattering cross section as a function of the scattering angle and not as a function of the momentum transfer.  Let θ be the angle between k and k'.  Then q = 2ksin(θ/2).