Lagrange multipliers

Assume you have chosen coordinates for a system that are not independent, but are connected by m equations of constraints of the form
Σ_ka_lk dq_k + a_lt dt =  0,  l = 1, ..., m.
Then the equations of motion can be obtained from

d/dt(∂L/∂(dq_k/dt)) -  ∂L/∂q_k = ∑_lλ_la_lk,  (n equations),   Σ_ka_lk dq_k + a_lt dt =  0  (m equations).

We have m + n equations and m + n unknowns, the n coordinates and the m λ's.  The λ_l are called the undetermined Lagrange multipliers,  ∑_lλ_la_lk is the generalized force of constraint associated with the coordinate q_k.

Link:  Hamilton's principle and Lagrange multipliers

Elastic scattering

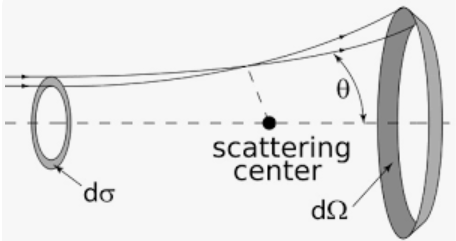
Consider the scattering of a particle by a central potential. 
We define the differential scattering cross section σ(Ω) = dσ/dΩ through the expression

# of particles scattered into the solid angle dΩ per unit time = I σ(Ω) dΩ,

where I is the intensity of the incident beam, i.e. the number of beam particles per unit area per unit time.
For a central potential σ(Ω) is independent of φ. 
We write σ(Ω) = σ(θ) = dσ/dΩ.
The number of particles scattered through an angle between θ and θ + dθ per unit time is
I σ(θ) 2π sinθ dθ.

We define the impact parameter b through
M = mv₀b = b(2mE)^½,
where M is the angular momentum and v₀ is the incident speed at infinite distance.
Once E and b are fixed, the scattering angle is uniquely determined.
A particle incident with impact parameter between b and b + db will be scattered through an angle between θ and θ + dθ.  We can write

I 2π σ(θ) sinθ dθ = -I 2π b db,
σ(θ) =|(b/sinθ)(db/dθ)|.

In a central potential the motion is in a plane and M and E are constant.
E = ½m(dr/dt)² + M²/(2mr²) + U(r) = ½m(dr/dt)² + b²E/r² + U(r), since M = mv₀b = b(2mE)^½.
dr/dt = ±[(2/m)(E(1 - b²/r²) - U(r))]^½.

M = mr²(dφ/dt),  d/dt = [M/(mr²)]d/dφ = [b(2mE)^½/(mr²)]d/dφ.

From dr/dt = [(2/m)(E(1 - b₂/r²) - U(r))]^½
we then find the equation for the trajectory.
dr/dφ = [(2/m)(E(1 - b²/r2) - U(r))]^½/ [b(2mE)^½/(mr²)]
= [(E½ (1 - b²/r²) - U(r))]^½/ (b/r²).
dφ/dr = (b/r²)/ [(E^½ (1 - b²/r²) - U(r))]^½.
dφ/du = -b/ [(E^½ (1 - b²u²) - U(u))]^½, with u = 1/r.

φ(u) = b∫₀^udu'/[1 - b²u'² - U(u')/E]^½, with φ(z = -∞) = 0.

Let θ be the angle between the incident and the scattered direction and φ₀ be the angle between r(z = -∞) and r_min.
Then
φ₀ = b∫₀^umaxdu'/[1 - b²u'² - U(u')/E]^½,
and
E = M²/(2mr²_min) + U(r_min) = b²E/r²_min + U(r_min) =  b²Eu²_max + U(u_max)
determines u_max.  We have
θ = π - 2φ₀ for a repulsive potential,
|θ| = 2φ₀ - π for an attractive potential, or θ = π - 2φ₀, θ < 0.

If U(r) = α/r, U(u) = αu, U(u_max) = αu_max, then
u_max = -α/(2b²E) + [α²/(4b⁴E²) + 1/b²]^½ and φ₀ = cot^-1(α/(2bE)).
cotφ₀ = α/(2bE),  cot(θ/2) = cot(π/2 - φ₀) = tanφ₀ = 1/cotφ₀.
b = [α/(2E)] cot(θ/2), db/dθ =  -½[α/(2E)]sin^-2(θ/2),
σ(θ) = ¼[α/(2E)]²sin^-4(θ/2).
This is the Rutherford's formula.

Frame transformations

Let θ be the scattering angle in the lab frame and θ₀ be the scattering angle in the CM frame.  The number of particles scattered into a detector is the same in the laboratory and in the CM frame.  Therefore
σ(θ) sinθ dθ = σ(θ₀) sinθ₀ dθ₀.