Maxwell's equations, boundary conditions for the electric and magnetic fields
The intensities of the reflected and transmitted waves are proportional to the squares of the corresponding electric field amplitudes. We find the ratio of these amplitudes to the incident amplitude by applying boundary conditions.
Let the film lie between the planes z = 0 and z = d.
At the interfaces the tangential components of E and H are continuous.
Let the wave be incident from z = -∞ and the polarization direction be the x-direction.
Let k = 2π/λ, ω = 2πc/λ. Define the positive direction for E as shown.
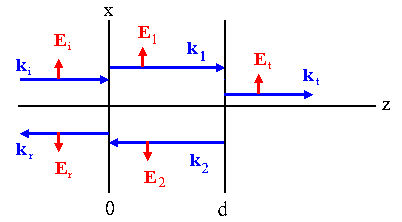
ki = kr = kt = k, k1 = k2
= nk.
For z < 0 we have
E(r,t) =
i [Ei exp(i(kz - ωt)) - Er
exp(i(-kz - ωt))],
B(r,t)
= j [Ei exp(i(kz - ωt)) + Er
exp(i(-kz - ωt))]/c,
H(r,t)
= B(r,t)/μ0.
In the film for 0 <
z < d we have
E(r,t) = i [E1
exp(i(nkz - ωt)) - E2 exp(i(-nkz
- ωt))],
B(r,t) = j [E1
exp(i(nkz - ωt)) + E1 exp(i(-nkz
- ωt))](n/c), H(r,t) = B(r,t)/μ0.
For z > d we have
E(r,t) = i
Et exp(i(kz - ωt)),
B(r,t)
= j Et exp(i(kz - ωt))/c. H(r,t)
= B(r,t)/μ0.
The boundary
conditions at z = 0 for the tangential component of E yield
Ei - Er = E1 - E2.
The
boundary conditions at z = 0 for the tangential component of H
yield
Hi + Hr = H1 + H2. H
= B/μ0 in all regions, B = En/c in the film, B = E/c outside the
film.
Ei + Er = n(E1 + E2).
Measuring all field strength in units of Ei we have express E1
and E2 in terns of Er.
Er = -E1 +
E2 + 1, Er = nE1 + nE2 - 1.
E2 = ((n + 1)Er - n + 1)/(2n), E1 = (n +
1 - (n - 1)Er)/2n.
The boundary conditions at z = d for the
tangential component of E yield
E1exp(inkd) - E2exp(-inkd)
= Etexp(ikd).
The boundary conditions at z = d for the tangential
component of H yield
H1exp(inkd) + H2exp(-inkd)
= Htexp(ikd).
nE1exp(inkd) + nE2exp(-inkd) =
Etexp(ikd).
-(n + 1)E2exp(-inkd) = (n - 1)E1exp(inkd).
Substituting E1 and E2 in terms of Er from
above we get
-(n + 1)((n + 1)Er - n + 1)exp(-inkd) = (n - 1)(n + 1
- (n - 1)Er)exp(inkd).
Er[(n + 1)2exp(-inkd)
- (n - 1)2exp(inkd)] = (n2 - 1)exp(-inkd) - (n2
- 1)exp(inkd).
Er[4n cos(nkd) + i2(n2 + 1) sin(kd)] =
-i(n2 - 1)2sin(kd).
R = |Er|2 = 4(n2
- 1)2sin2(kd)/[16n2 cos2(nkd) + 4(n2
+ 1)2 sin2(kd)].
R = (n2 - 1)2/[4n2
cot2(nkd) + (n2 + 1)2]
is the reflectance,
i.e. the fraction of the incident energy that is reflected.