Problem 2:
Determine the E and B fields of an electric dipole moving along the z-axis with a velocity v = v k relative to the laboratory using the Lorentz transformation of the fields. The dipole moment in its rest frame is p = p0 k.
Solution:
- Concepts:
The dipole field, the transformation of E and B from one Lorentz frame to another - Reasoning:
In the rest frame of the dipole, with the dipole at the origin,
E(r,t) = (1/(4πε0)) (1/r3)[3(p∙r)r/r2 - p], B(r,t) = 0.
p = p0 k. We have axial symmetry about the z-axis.
Let us find the components of the electric field parallel and perpendicular to the z-direction.
3(p∙r)r/r2 - p = 3p0cosθsinθ (ρ/ρ) + 3p0cos2θ k - p0 k = 3p0cosθsinθ (ρ/ρ) + p0(3cos2θ - 1) k
= 3p0ρz/(ρ2 + z2) (ρ/ρ) + p0(2z2 - ρ2)/(ρ2 + z2) k.
E(r,t) = (1/(4πε0)) (1/(ρ2 + z2)5/2)[3p0ρz (ρ/ρ) + p0(2z2 - ρ2) k]. - Details of the calculation:
The laboratory frame is moving with speed v = -v k with respect to the rest frame of the dipole.
We find the fields in the laboratory frame using
E'|| = E||, B'|| = B||, E'⊥ = γ(E + v×B)⊥, B'⊥ = γ(B - (v/c2)×E)⊥.
E'|| = (1/(4πε0)) (1/(ρ2 + z2)5/2)p0(2z2 - ρ2) k. B'|| = 0.
z = γ(z' - vt'), ρ = ρ'.
E'|| = (1/(4πε0)) (1/(γ2(z' - vt')2 + ρ'2)5/2)p0(2γ2(z' - vt')2 - ρ'2) k.
E'⊥ = γE⊥ = (γ/(4πε0)) (1/(ρ2 + z2)5/2)3p0ρz (ρ/ρ)
= (γ2/(4πε0)) (1/(γ2(z' - vt')2 + ρ'2)5/2)3p0ρ'(z' - vt') (ρ/ρ).
B'⊥ = -γ(v/c2)×E = -(v/c2)(γ3/(4πε0))(1/(γ2(z' - vt')2 + ρ'2)5/2)3p0ρ'(z' - vt') (φ/φ).
Problem 3:
(a) A fast electron (kinetic energy = 5*10-17
Joule) enters a region of space containing a
uniform electric field of magnitude E = -i 1000 V/m. The field is parallel to the electron's motion
and in a direction such as to decelerate it. How far does the electron travel
before it is brought to rest? Neglect radiation losses.
(b) Now assume that the initial velocity of the electron is
v = v0j,
perpendicular to the direction of the electric field. Assume that at t = 0
the electron moves through the origin. Find the speed of the electron, its
position, and the work done by the field on the electron as a function of time.
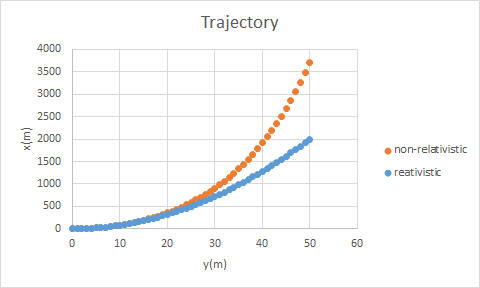
(c) Find the trajectory of the electron, x(y).
Solution:
- Concepts:
F = dp/dt, p = γmv. - Reasoning:
The electron is acted on by a constant force. We neglect radiation losses. - Details of the calculation:
(a) E = E i, q = -1.6*10-19 C.
dpx/dt = qE, dpy/dt = dpz/dt = 0.
px(t) = p0 + qEt, py(t) = pz(t) = 0.
Note: both q and E are negative, so qE is positive.
This part of the problem can be treated non-relativistically,
since 5*10-17 J << mc2 = 0.511 MeV * 1.6*10-13 J/MeV.
vx = v0 - qEt/m = 0 --> t = v0m/(qE).
x = v0t - ½at2 = ½mv02/(qE) = (5*10-17 J)/(1.6*10-19 C * 1000 N/C) = 0.3125 m.
(b) dpx/dt = qE, dpy/dt = dpz/dt = 0.
pz(t) = 0, px(t) = qEt, py(t) = p0.
Energy Et(t) = (m2c4 + p2c2)½ = (Et02 + (qcEt)2)½.
Et02 = m2c4 + p02c2.
Notation: Et denotes the total energy, E denotes the field strength.
Et = γmc2, p = γmv, v/c = pc/Et.
vx(t)/c = cqEt/(Et02 + (qcEt)2)½, vy(t)/c = cp0/(Et02 + (qcEt)2)½.
dx/dt = c2qEt/(Et02 + (qcEt)2)½, x(t) = (qE)-1∫0qcEt t'dt'/(Et02 + t'2)½.
x(t) = (qE)-1(Et02 + (qcEt)2)½ - Et0/(qE).
dy/dt = c2p0/(Et02 + (qcEt)2)½ = c2p0Et0/(1 + (qcEt/Et0)2)½.
y(t) = (c2p0/Et0) ∫0u dt'/(1 + t'2)½, with u = qcEt/Et0.
y(t) = (p0c/(qE)) sinh-1(qcEt/Et0).
The work done on the electron by the field is
W(t) = (Et02 + (qcEt)2)½ - Et0.
(c) Express t in terms of y(t): sinh(qEy/(p0c)) = qcEt/Et0.
x(t) = Et0(qE)-1(1 + (qcEt/Et0)2)½ - Et0/(qE).
x(y) = [Et0/(qE)][(1 + sinh2(qEy/(p0c)))½ - 1] = [Et0/(qE)] [(cosh(qEy/(p0c)) - 1].
Et0 = mc2 + T = 8.18*10-14 J, qE = 1.6*10-16 N, Et0/(qE) = 511 m,
p0c = 2.86*10-15 J, qE/(p0c) = 0.056/m.
x(y) = 511 m (cosh(y*0.056/m) - 1).

Problem 4:
A reference frame K' is moving with uniform velocity v = vi
with respect to reference frame K.
(a) In K, a plane wave with angular
frequency ω is traveling in the i direction. What is its frequency in K'?
(b) In K, a plane wave with angular frequency ω is traveling in the
j
direction. What is its frequency in K'?
(c) In K, a plane wave with
angular frequency ω is traveling in a direction making an angle of 45o
with respect to the i direction and the j direction. What is its
frequency in K'?
Solution:
- Concepts:
The relativistic Doppler shift - Reasoning:
Given the angular frequency ω of a plane wave in reference frame K we are asked to find the angular frequency ω' in reference frame K' moving with constant velocity with respect to K. - Details of the calculation:
(a) ω' = ω[(1 - v/c)/(1 + v/c)]½ if k and v are parallel to each other.
(b) ω' = γω if k and v are perpendicular to each other. γ = (1 - v2/c2)-½.
There is a transverse Doppler shift, even if θ = π/2.
(c) ω' = γ(ω - v·k) = γω(1 - vcosθ/c) = γω(1 - v/(√2c)).