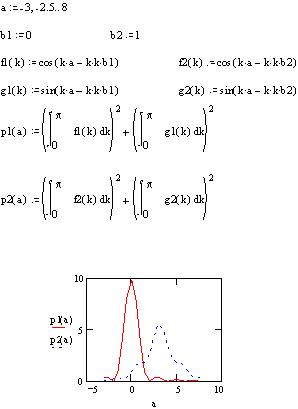Spreading of a wave packet
We can terminate the Taylor series expansion
β(k) = β(k⁰) + (k - k₀)dβ(k)/dk|_k0 + ½(k - k₀)²d²β(k)/dk²|_k0  + ...
after the first term if all higher order terms are much smaller than 2π.  However, as t increases, the higher order terms increase steadily with t.  Therefore the second order term must be included for times greater than some t₁.
We have
d²β(k)/dk²|_k0 = d²α(k)/dk²|_k0 + d²ω(k)/d²k|_k0t,   d²ω(k)/d²k =  ħ/m.
Therefore d²β(k)/dk²|_k0 depends on t, and for large enough times t its magnitude increases with time.
The wave packet is the of the form
Ψ(x,t) ∝ ∫|g(k)| exp(i((k - k₀)(x - x₀ - v_gt) - (k - k₀)²x₁) dk,   x₁ = -½d²β(k)/dk²|_k0.
x₁ depends on t, and for large enough times t its magnitude increases with time.
Ψ(x,t) ∝ ∫|g(k)| exp(i2π(k - k₀)/τ) dk,  with  τ = 2π/((x - x₀ - v_gt) - (k - k₀)x₁).
Now |x - x₀ - vt |>> Δk^-1 is no longer sufficient for |τ| << Δk. 
We need |(x - (k - k₀)x₁) - x₀ - vt | >> Δk^-1 for the integrand to oscillate rapidly and the contribution to the integral to be zero. 
The width of the wave packet increases with time.

Example:
Let |g(k)| = 1 for k₀ < k < (k₀ + π).  Then
Ψ(x,t) ∝ ∫_k0^k0+π exp(i(k - k₀)(x - x₀ - v_gt) - (k - k₀)²x₁) dk
= ∫_k0^k0+π cos((k - k₀)(x - x₀ - v_gt) - (k - k₀)²x₁) dk + i∫_k0^k0+π sin((k - k₀)(x - x₀ - v_gt) - (k - k₀)²x₁) dk.
P(x,t) = |ψ(x, 0)|² = [∫_k0^k0+π cos((k - k₀)(x - x₀ - v_gt) - (k - k₀)²x₁) dk]²
+ [∫_k0^k0+π sin((k - k₀)(x - x₀ - v_gt) - (k - k₀)²x₁) dk]².
Let x - x₀ - v_gt = a, x₁ = b.
Compare P(x,t) at t = 0 when b = 0 and at some later time when b ≠ 0.

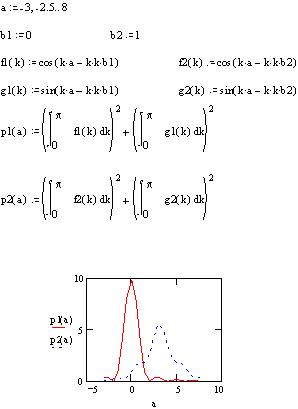
Problem:
In one dimension, at t = 0 the normalized wave function of a free particle of mass m in k-space is
Φ(k,0) = N exp(-k²/(2b²)).
(a)  Find the normalization constant N.  Find the expectation value <p> = ħ<k>.
(b)  Find the FWHM in of |Φ(k,0)|² in k-space.
(c)  Find the corresponding wave packet Ψ(x,0) in coordinate space.  Find <x>.
(d)  Find the FWHM in of |Ψ(x,0)|² in coordinate space.
(e)  Find the FWHM in of |Ψ(x,t)|² an some later time t.  Does it change with time?
(f)  Find the FWHM in of |Φ(k,t)|.  Does it change with time?

Hint:  ∫_-∞^+∞exp(-a²(x + c)²)dx = √π/a

Solution:

• Concepts:
  Postulates of QM, the Fourier transform
• Reasoning:
  We investigate the properties of a Gaussian wave packet representing a free particle.
• Details of the calculation:
  (a)  N²∫_-∞^+∞exp(-k²/b²)dk = 1.  ∫_-∞^+∞exp(-k²/b²)dk = b√π,
  N = 1/(b√π) ^½.  <p> = <k> = 0.
  (b)  exp(-k²/b²) = ½,   k = b√(ln2),  FWHM = 2√(ln2)b.
  (c)  Ψ(x,0) = [1/(2π)^1/2][1/(b√π)^1/2] ∫_-∞^+∞exp(-k²/(2b²))exp(ikx) dk.
  Let us group the k-dependent terms into a perfect square.
  -k²/(2b²) + ikx = [-1/(2b²)][k – ixb²]² - x²b²/2,
  Integrating we find
  Ψ(x,0) = (b²/π)^1/4exp(-x²b²/2).  <x> = 0.
  (d)  exp(-(x-x₀)²b²) = ½.   FWHM = 2√(ln2) (1/b).
  (e)  Ψ(x,t) = [1/(2π)^1/2][1/(b√π)^1/2] ∫_-∞^+∞exp(-k²/(2b²))exp(i(kx – ωt)) dk.
  E = ħω = ħ²k²/(2m),  ω = ħk²/(2m).  dω/dk = ħk/(m) = v_g.
  -k²/(2b²) + i(kx – ħk²t/(2m))  = -A[k – ix/2A]² – x²/(4A),
  where A = 1/(2b²) + iħt/(2m).
  Integrating we find
  Ψ(x,t) = [1/(2π)^1/2][1/(b√π)^1/2] √(π/A) exp(-x²/(4A))
   = (4/(b²π))^1/4 e^iφ/(4/b⁴ + 4(ħt/m)²)^1/4 exp(-x²/(2/b² + 2iħt/m)), 
  where φ is real and independent of x.
  Here
  [1/(2π)^1/2][1/(b√π)^1/2] √(π/A) = (4/(b²π))^1/4 √(1/(4A)) = (1/(b²π))^1/4 |√(1/(4A))|e^iφ.
  |Ψ(x,t)|² = (4/(b²π))^1/1 1/(4/b⁴ + 4(ħt/m)²)^1/2 exp(-(4x²/b²)/(4/b⁴ + 4(ħt/m)²)). 
  exp(-(4x²/b²)/(4/b⁴ + 4(ħt/m)²)) = ½.   FWHM = 2√(ln2)(1/b)(1 + b⁴(ħt/m)²)^1/2.
  The FWHM of |Ψ(x,t)|² increases with time
  (f)  Φ(k,t) = exp(-iωt)) Φ(k,0). 
  FWHM of |Φ(k,t)| = 2√(ln2)b.  It does not change with time.

Summary
The wave function of a free particle is a wave packet.  The center of this wave packet moves with constant velocity v_g, called the group velocity.  The width of the wave packet increases with time, the wave packet spreads, we gradually loose position information.