The Hamiltonian for the positronium atom in the 1S state in a magnetic field B is, to a good approximation,
,
where 1 labels the electron and 2 the positron. Here S1 and S2 are the spin operators for the two particles and A is a constant.
(a) Choose the z-axis along B. Which of the following are constants of motion?
1. S12 and S22
2. S1z and S2z
3. S2
4. S=S1+S2
5. Sz=S1z+S2z
(b) Find the energy eigenvalues of H in terms of the constants A
and 
.
(a) The positronium atom consists of two spin ½ particles. We neglect the spatial motion of the particles and consider only spin interactions. The first term in the Hamiltonian is the spin-spin interaction, and the second term is the interaction of the spins with an external magnetic field.
.
In the { |S,Sz> } basis the matrix of S1×S2 is diagonal, while the matrix of 
is diagonal in
the {|++>,|+->,|-+>,|-->} basis. Let us work in the {|++>,|+->,|-+>,|-->}
basis.
Then the matrix of S1×S2 is
,
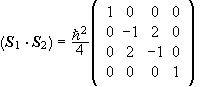and the matrix of S1z - S2z is
.
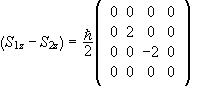The matrix of H therefore is
,
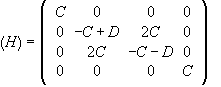where 
.
To find out if an observable is a constant of motion, we have to find out if it commutes with the Hamiltonian H. If it commutes, it is a constant of motion.
1. 
.
2. The matrix of S1z is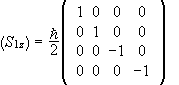 
.
The matrix of S2z is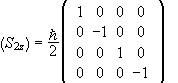 
.
S1z, S2z, and H do not have a set of common
eigenvectors. Therefore 
.
3. The matrix of S2 is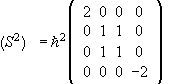 
. 
.
4. The matrix of S1x +S2x is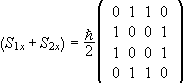 
.
The matrix of S1y +S2y is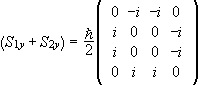 
.
The matrix of S1z +S2z is 
.
.
S1+S2 is not a constant of motion.
5. Sz=S1z+S2z is a constant of motion.
(b) The eigenvalue of H are found from E=C or fromE2+2CE+C2-D2-4C2=0.
.
An electron (charge -e, and magnetic moment m) moves through a magnetic field.
(a) Write the Hamiltonian for this particle (assume non-relativistic kinematics). Give m for the electron in Bohr magnetons.
(b) Now ignore the charge and spatial motion of the particle. Assume a constant
magnetic field B0 in the y-direction. Write the
Schroedinger equation for the spin state vector, explicitly giving the Hamiltonian.
At
time t=0 the spin state is 
.
By solving the time-dependent Schroedinger equation in which one defines 
show that the
state at time t1 such that 
is 
.
(c) Suppose that a neutron in this spin state passes between the two poles of a magnet. If B is inhomogeneous and in the x-direction, find the probability that the neutron will be found in the spin down state (in the x-direction) after passing the gap between the poles of the magnet.
(a) The intrinsic magnetic moment of a particle
is 
.
For an
electron 
, where 
is the Bohr magneton 
in Gaussian units.
In SI units the Hamiltonian of the particle is
,
where
, 
, 
.
.The matrix of H
is 
.
The energy eigenvalues are found from 
.
Let 
.
Let 
.
.
.
.
.
It is passed through the analyzer, which measures the Sx component.
The
probability that the neutron will be found in the spin down state is 
.
An atom with L=0 and S=½ is initially in its ground
state with Sz =-½ . A field 
is turned on at t=0 so that the
effective Hamiltonian may be taken to be
,
where H0 is the atomic Hamiltonian with H1 = 0. Thus both Sz=½ and Sz=-½ states have the same eigenvalue of H0 in the ground state.
(a) What is the probability P, to lowest order in H1, that the atom remains in the state |S=½,Sz=-½ > at time t?
Here 
, e is the
magnitude of the electron charge, me is the electron mass, and c
is the velocity of light in the vacuum.
(b) Under what conditions on t will P=0?
(a) Assume that the energy of the twofold degenerate
ground state is much lower than the energy of any excited state, and approximate the
system by a two-level system.
Denote the two levels by |+> and |->. H0|+>=E0|+>,
H0|->=E0|->, the system is degenerate.
{|+>,|->} are the eigenstates of Sz. 
.
At t=0 the system is in the state |->, but the Hamiltonian is H0+W=H, with
.
In the {|+>,|->} the matrix of W is
.
The matrix of H is
.
The eigenvalues of H are 
,
and the corresponding eigenfunctions are
.
In this problem 
.
.
.
.
If 
then 
.
with n an odd
integer, then 
.The Hamiltonian of a system of two spin ½ particles may be written as
,
where S1 and S2 are the spin matrices for particle 1 and 2 respectively.
(a) Show that H commutes with the square of the total spin operator and the z-component of the total spin.
(b) Find the eigenspinors and eigenenergies of this Hamiltonian.
(a) The first term (A) is the part of the Hamiltonian that does not depend on
spin, the second term is the spin-spin interaction, and the third term is the interaction
of the spins with an external magnetic field. In the {|S,Sz>} basis the
matrices of 
are diagonal.
,
.
, 
.
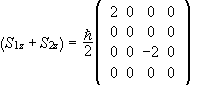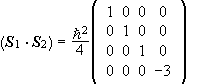The matrix of H is therefore diagonal and the matrix of S2 is diagonal.
, 
.
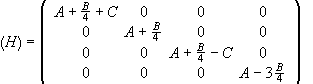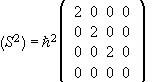Since all these matrices are diagonal, they all commute with each other.
(b) The eigenvalues of H are the diagonal matrix elements. The eigenvectors are the corresponding basis vectors,
and 
.