

The state space E(k,j,m) can be considered a direct sum of the orthogonal subspaces E(j,m), where m varies in integral jumps from -j to +j and j takes on all the values actually found in the problem. The dimension of each subspace is g(j). (Here each vector in a subspace E(j,m) has the same j and m but a different index k.)
We can also consider E(k,j,m) to be the direct sum of all orthogonal subspaces E(k,j) spanned by vectors with the same k and j but different indices m. The dimensions of these subspaces are 2j+1, and the subspaces are globally invariant under the action of all components of J. Any component of J acting on a vector in E(k,j) yields another vector in E(k,j) .
What are the matrices of Jz, J+, and J- in E(k,j)?
![]() .
.
![]() .
.
![]() .
.
The matrix elements in E(k,j) therefore are
![]() ,
,
![]() .
.
The matrix elements are independent of the value of k, they depend only on j and m, they are "universal". They do not depend on a particular physical system.
The subspaces E(k,j) are one dimensional, the only possible value for m is zero. All matrices reduce to one element, which is zero.
In the { |+½>, |-½> } basis we have
![]() ,
,
![]() ,
,
![]() .
.
In the { |1>, |0>, |-1> } basis we have
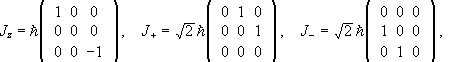
 .
.
![]() .
.
![]() .
.
![]() .
.
![]() ,
,
with the center of the charge distribution at the origin of the coordinate system. Here
![]() .
.
A nucleus with a quadrupole moment has a quantum mechanical charge density raJM(r)µ|yaJM(r)|2, which depends on the quantum numbers J and M. The quadrupole moment and the energy of the nucleus in an electric field gradient therefore depend on J and M.
Consider a nucleus with a quadrupole moment and with angular momentum l=1. Assume that the Hamiltonian of the nucleus may be written as
![]() ,
,
where Lu and Lv are the components of L
along the two directions ![]() in the x-z plane which form angles of 45o with the x-
and z-axes and
in the x-z plane which form angles of 45o with the x-
and z-axes and ![]() is a constant.
is a constant.
(a) Write the matrix of H in the { |1>, |0>, |-1> } basis. What are the stationary states of the system and what are their energies? Write these states as |E1>, |E2>, and |E3>, in order of decreasing energy.
(b) At time t=0 the system is in the state ![]() . What is the state vector |y(t)> at time t? At time t Lz
is measured? What are the probabilities of the various possible results?
. What is the state vector |y(t)> at time t? At time t Lz
is measured? What are the probabilities of the various possible results?
(c) Calculate the mean values <Lx>(t), <Ly>(t), and <Lz>(t). What is the motion performed by the vector <L>?
(d) At time t Lz2 is measured. Do times exist when only one result is possible? Assume that the measurement yielded h2. What is the state of the system immediately after the measurement? Indicate, without calculation, its subsequent evolution.
(a) ![]() .
. ![]() .
.
![]() .
.
![]() .
.
![]()
![]() .
.
![]() .
.
![]() .
.
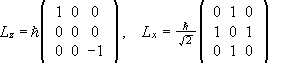 in the { |1>, |0>,
|-1> } basis.
in the { |1>, |0>,
|-1> } basis.
 .
.
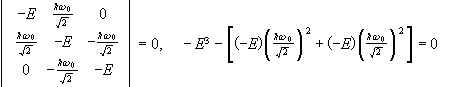 .
.
![]() .
.
Assume ![]() is positive. Then
is positive. Then
![]() .
.
![]() .
.
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() .
.
(c)
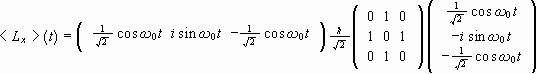
=0.
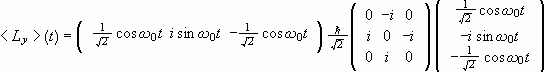
![]() .
.
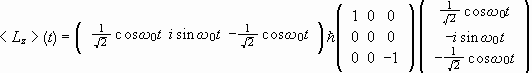
=0.
or
![]() .
.
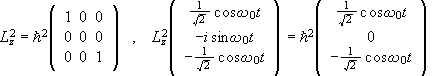 .
.At ![]() and |y(t)>
is an eigenvector of Lz2 with eigenvalue
h2.
and |y(t)>
is an eigenvector of Lz2 with eigenvalue
h2.
At ![]() and |y(t)>
is an eigenvector of Lz2 with eigenvalue 0.
and |y(t)>
is an eigenvector of Lz2 with eigenvalue 0.
After a measurement of h2
the state
of the system is the eigenstate of Lz2 ![]() . This state evolves like |y(0)>.
. This state evolves like |y(0)>.
Show that if any operator commutes with two of the components of an angular momentum operator, it commutes with the third.
Solution:
Details of the calculation:
Let i ≠ j,k j ≠ k and let i, j, k be cyclic ( x, y, z or y, z, x or z, x, y ).
Then
[Ji,Jj] = iħJk, JiJj
- JjJi = iħJk.
Let A be an operator.
Assume
[Ji,A] = 0, [Jj,A] = 0. Then [A, Jk]
= (1/iħ)[A,JiJj
- JjJi].
iħ[A,
Jk] = [A,JiJj]
- [A,JjJi]
= [A,Ji]Jj
+ Ji[A,Jj]
- [A,Jj]Ji
- Jj[A,Ji]
= 0.
Consider the so-called spin Hamiltonian ![]() , for a system of spin 1. Show that the
Hamiltonian in the Sz basis is
, for a system of spin 1. Show that the
Hamiltonian in the Sz basis is 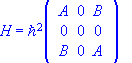 .
Find the eigenvalues of this Hamiltonian.
.
Find the eigenvalues of this Hamiltonian.
For a spin 1 system we choose as the basis vectors the eigenstates of Sz,
{ |1>, |0>, |-1> } with eigenvalues ![]() respectively.
In this basis the matrix for Sz is
respectively.
In this basis the matrix for Sz is
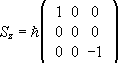 .
.
The matrices for Sx and Sy are
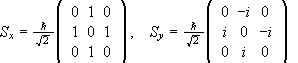 .
.
Therefore
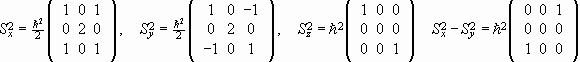 ,
,
 .
.
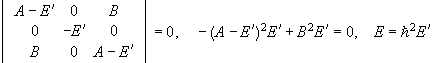 .
.
We have ![]() .
.
The eigenvalues and eigenvectors are:

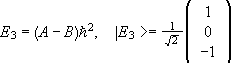 .
.