Problems

Problems:

Consider a system of angular momentum j=1, whose state space is spanned by the common eigenvectors of J2 and Jz ,{ |1>, |0>, |-1> }, with eigenvalues of Jz of , 0, and - respectively.
The state of the system is |y>=a|1> + b|0> + c|-1>.

(a)  Calculate the mean value <J> of the angular momentum in terms of a, b, and c.

(b)  Give the expressions for <Jx2>, <Jy2>, and <Jz2> in terms of the same quantities.

Solution:

(a)  In the { |1>, |0>, |-1> } basis the matrices of Jx, Jy, and Jz are

Image3501.gif (2202 bytes).

The vector |y> is represented by the column matrix .

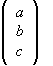Assume |y> is normalized and |a|2+|b|2+|c|2=1.

.

Similarly,

.

(b)  The matrices for Jx2, Jy2, and Jz2 are

.

,

.

.

 

Consider a system whose four-dimensional state space is spanned by a basis of common eigenvectors of J2 and Jz , { |1,1> |1,0>, |1,-1>, |0,0> } with j=0 or 1.

(a)  Express the common eigenstates of J2 and Jx in terms of the eigenstates of J2 and Jz.

(b)  Consider a system in the normalized state |y>=a|1,1> + b|1,0> + c|1,-1> + d|0,0>.

   i)  What is the probability of finding 2 and if J2 and Jz are measured simultaneously?

   ii)  Calculate the mean value of Jz and the probabilities of the various possible results.

   iii)  Answer the same questions for J2 and Jx .

   iv)  If Jz2 is measured, what are the possible results, their probabilities and their mean value?

Solution:

(a)  The basis vectors are { |1,1> |1,0>, |1,-1>, |0,0> }.  In this basis the matrices for  Jx, Jy,Jz,J+,J-, and J2  are

,

.

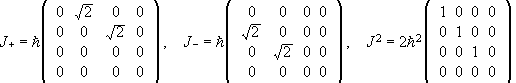To find the eigenvalues b of Jx we require .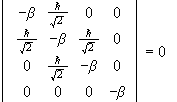

 .

The eigenvalue b=0 is twofold degenerate.

The associated eigenvectors are

  J2 Jx
b=0: |0,0> 0 0
2 0
2
2 -
 

(b) |y>=a|1,1> + b|1,0> + c|1,-1> + d|0,0> = .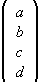
|a|2+|b|2+|c|2+|d|2=1.
(i)  .
(ii)  .
(iii) 

.

 as on the previous line.

.

.

iv) The possible results of measuring Jz2 are 0 and .

.

For a simple particle moving in space, show that the wave function ylm(r)=x2+y2-2z2 represents a simultaneous eigenstate of L2 and Lz with eigenvalues l(l+1)and m . Determine l and m.  Find a function with the same eigenvalue for L2 and the maximum possible eigenvalue for Lz.
Solution:
.

Express ylm(r) in terms of the spherical harmonics.

.

ylm(r) is an eigenfunction of Lz with eigenvalue 0 and an eigenfunction of L2 with eigenvalue 6 ( l=2 ). For l=2 the maximum possible eigenvalue of Lz is m=2.

The corresponding eigenfunction is .

 

A system has a wave function , with a real.  If Lz and L2 are measured, what are the probabilities of finding 0 and 2?
Solution:
Express the wave function in terms of spherical harmonics.

.

.

.

.

                                                 

 for properly chosen N.

.

Let P(l,m) denote the probability of finding the eigenvalues l(l+1) and m .

.

 

Consider a charged particle on a ring of unit radius with Hamiltonian .

The units are chosen such that =2m=1.  Find the complete set of eigenvalues and eigenfunctions.

Solution:

.

Try . .

We need .

.

 

A particle is known to be in an eigenstate of L2 and Lz.  Prove that the expectation values satisfy

.

Solution:

.

.

.

.

The only matrix elements that can be nonzero are the matrix elements of .

Therefore .

.