Review

The operator J, whose Cartesian components satisfy the commutation relations is defined as an angular momentum operator.  For such an operator we have [J_i,J²]=0, i.e. the operator J²=J_x²+J_y²+J_z² commutes with each Cartesian component of J.  We can therefore find an orthonormal basis of eigenfunctions common to J² and J_z.  We denote this basis by {|k,j,m>}. We have .

The index j can take on only integral and half integral positive values.  Which integral and half integral values of j are allowed depends on the exact nature of the physical problem.  For a given j the index m can take on one of 2j+1 possible values, m=-j,-j+1,... ,j-1,j.

We define the operators J₊=J_x+iJ_y  and J_-=J_x-iJ_y.  We then have and .

The operators J± operating on the basis states {|k,j,m>} yield

.

Orbital angular momentum

The operator L=R´P satisfies the commutation relations and is called the orbital angular momentum operator.  We denote the common eigenstates of L² and L_z by {|k,l,m>}.

Problem:

• Solution:

  (a) Let the vectors {|k,1,1>,|k,1,0>,|k,l1,-1>} be the eigenvectors of L_z with eigenvalues respectively, which span the subspace E(k,l) with l=1. After the measurement of L² and L_z the particle is in state |k,1,1>. E(k,l) is invariant under L. The matrix of L_y in the above basis is

  .

  It can be constructed using  and  ,

  .

  The eigenvalues of L_y are ,

  where .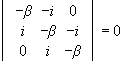

  We have    .

  For the eigenvalue 0 we have

  .

  For the eigenvalue we have

  .

  For the eigenvalue we have

  .

  (b) ,

  ,

  .

  • Note: k may denote the energy of the free particle.  If the particle does not have a well defined energy then the state of the particle after the measurement of L² and L_z is

    ,

    with

    .

Let |y> be an arbitrary state vector, and let the result of operating with L_x on |y> be |f>, i.e. L_x |y>=|f>.  In coordinate representation we write

.

.

.

In coordinate representation the operator L_x is therefore written as

.

Similarly,

.

It is often more convenient to work in spherical coordinates, r, q, f;

  are the relationships between Cartesian coordinates and spherical coordinates.  Each spherical coordinate is a function of x, y, and z and each Cartesian coordinate is a function of r, q, f.  We can derive the relationships between the partial derivatives

.

.

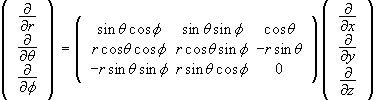Inverting the matrix we find

.

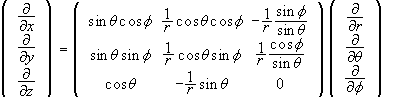Therefore

Similarly,

.

This yields L²=L_x²+L_y²+L_z²,

.

.

In coordinate representation the eigenfunction associated with the eigenvalues and of L² and L_z respectively are therefore solutions to the partial differential equations

,

with l integral or half integral and m=-l,-l+1,...l-1,l.

The variable r does not appear in any differential operator.  We may therefore separate variables and look for solutions of the form

.  We will show that the are unique.

To have a normalized wave function we need

.

It is convenient to normalize in the following way

, .

The normalized common eigenfunctions of L² and L_z are called the spherical harmonics.

Properties of the spherical harmonics

• (a)  .

  Separation of variables is possible.  We look for solutions of the form .

  Wave functions must be continuous at all points in space.  We therefore need
  .
  In the case of orbital angular momentum the nature of the physical problem dictates that m must be an integer, and therefore l must be an integer.

• (b)
  from the general theory.

  .

• .

  .

  Y_ll is uniquely defined up to the arbitrary constant c_l.

  determines |c_l|.

  .  It is customary to choose the phase of c_l such that .

    is thus uniquely determined.

• (c)

  allows us to construct all from .  The are thus uniquely defined. To each pair (l,m) there corresponds one and only one eigenfunction .

  .

  But we also have

  .

  Therefore

  .

  We have

  ,

  .

  The may be written as products of the associated Legendre functions and .

  ,

  ,

  where , and P_l(u) is the lth order Legendre polynomial.

  Note: The choice of phase for the P_lm(u) and therefore the definition of the Y_lm in terms of the P_lm is not unique.

The form a complete set of functions of f and the form a complete set of functions of cosq, therefore the form a complete set of functions of angle on the unit sphere.  Orthonormality is expressed through , and completeness is expressed through .

We can expand an arbitrary function f(q,f) in the series

 with .

Most mathematical tables list properties of the spherical harmonics.  You need to be aware of these properties, so that you can look them up as needed.

.

.  This can be derived from the expression of the Y_lm in terms of the .

.

real positive number.  This is guarantied by the choice of c_l.

, with .

The parity operator operating on a function of the coordinates replaces in this function the coordinates of any point in space by those of the point which is obtained by reflection through the origin of the coordinate system.

 in Cartesian coordinates,

 in spherical coordinates.

.

.

The parity of the spherical harmonics is well defined and depends only on l.

Links:

• Photographs
• 3-d interactive spherical harmonics
• The gallery page

Consider a particle whose state is described by .  We may expand y in terms of the eigenfunctions of L² and L_z.  .

Operating on these eigenfunctions with L_± yields .

We know that the y_klm(r) are of the form .

Therefore operating with L_± also yields  .

Comparison shows that R_klm±1(r)=R_klm(r), i.e. that R_klm(r) is independent of m.

We therefore write .

If [H,L]=0, then we can find common eigenfunctions of H, L², and L_z.  The eigenvalues E_kl of H and the radial function R_kl(r) are then independent of m.