Non-relativistic quantum description of particles with spin

The operator associated with the spin of a particle is a vector observable.  Its components satisfy the commutation relations that define an angular momentum operator.  The quantum state of a particle with spin is not completely specified by specifying its wave function ψ(r) in orbital space E_r.  We must also specify its spin variables in spin space E_s.  A given particle is characterizes by a unique value of s, which is a positive integer or half integer.  (2s + 1) basis vectors span the spin space E_s of this particle.  We can choose these basis vectors to be {|s,m_s>, m_s= -s, -s+1, ..., s}, the eigenvectors of S² and S_z.  The state space of the particle is the tensor product space E = E_r ⊗ E_s.  The spin observables commute with all the orbital observables.

For the electron E_s is two-dimensional.  The observables {X,Y,Z,S²,S_z} form a C.S.C.O. in E = E_r ⊗ E_s.  So do the observables {P_x,P_y,P_z,S²,S_z}. 
Since {|r>} forms a basis for E_r and {|ε>,|ε> = |+>,|->} forms a basis for E_s, {|r> ⊗ |ε> = |r,ε>} forms a basis for E for a spin ½ particle. 
Each vector |r,ε> is a common eigenvector of X, Y, Z, S², and S_z.  We have
X|r,ε> = x|r,ε>,  Y|r,ε> = y|r,ε>,  Z|r,ε> = z|r,ε>,  S²|r,ε> = (3/4)ħ²|r,ε>,  S_z|r,ε> = εħ|r,ε>.
<r',ε'|r,ε> = δ_εε'δ(r - r'), (normalization)  Σ_ε∫d³r|r,ε><r,ε| = I,  (completeness).
For any vector |ψ> we have |ψ> = Σ_ε∫d³r|r,ε><r,ε|ψ> = Σ_ε∫d³r ψ(r)|r,ε>, with ψ(r) = <r,ε|ψ>.

Notation:
Let ψ₊(r) = <r,+|ψ>,  ψ_-(r) = <r,-|ψ>,  and let

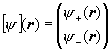
be a two component spinor, with its adjoint [ψ]^† = (ψ₊*(r), ψ_-*(r)).
For a spin ½ particle |ψ> is completely specified by the two component spinor, just as for a spinless particle |ψ> is specified by the wave function ψ(r).  The inner product is defined through
<ψ|Φ> = Σ_ε∫d³r|<ψ|r,ε><r,ε|Φ> = ∫d³r(ψ₊*(r)Φ₊(r) + ψ_-*(r)Φ_-(r)) = ∫d³r[ψ]^†[Φ].
Note: Matrix multiplication of the spinors precedes the spatial integration.
The state is normalized in the following way:
<ψ|ψ> = ∫d³r(ψ₊*(r)ψ₊(r) + ψ_-*(r)ψ_-(r)) = 1.

The spinor associated with a tensor product vector |ψ> = |Φ> x |Χ> 
with |Φ> = ∫d³r Φ(r)|r> in E_r and |Χ> = c₊|+> + c_-|-> in E_s is

Note: Not all vectors in E are tensor product vectors.

Let |ψ> be the state of a spin ½ particle and let |ψ’> be obtained from |ψ> through the action of a linear operator A,  A|ψ> = |ψ’>.
We can associate with each linear operator A a 2 x 2 matrix [A] such that [A][ψ](r) = [ψ’](r).

Examples:

• Let A be a spin operator, say S₊.  We have

  ,

  

  .

  .

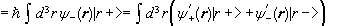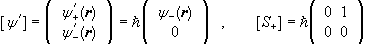  The matrix of a spin operator is its matrix in the { |+>, |-> } basis in E_s.

  Similarly, if A = S_z then

  .

• Let A be an orbital operator, say X.

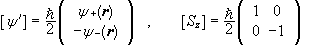  We have

  ,

  .

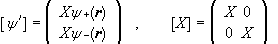  The matrix of an orbital operator is diagonal.

• Let A be a mixed operator, say L_zS_z.

  

  .

   

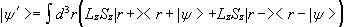
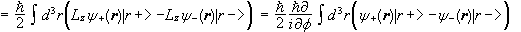  Similarly, if A = XS₊ , then

  .

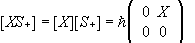Rotation operators for a spin ½ particle

Consider a system consisting of a single spin ½ particle.  Neglect the spatial degrees of freedom.  Rotate the system ccw about the z-axis through an angle φ.  If the state of the system is |α> before the rotation, it is |α>_R after the rotation, where |α>_R = U(R)|α>,   U(R) = exp(-iS_zφ/ħ) = exp(-iσ_zφ/2).
Before the rotation the expectation value of the operator S_x is <S_x> = <α|S_x|α>, after the rotation it is <S_x>_R = _R<α|S_x|α>_R.  We may expand

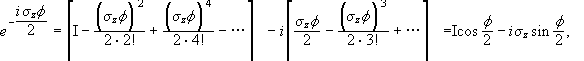
since σ_z² = I.  The expression for U^†(R)S_xU(R) therefore may be written

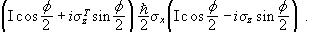
In matrix notation we have

.

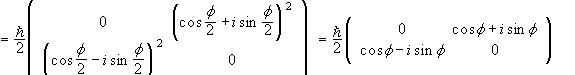
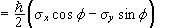Therefore  _R<α|S_x|α>_R = <α|U^†(R)S_xU(R)|α> = <α|S_xcosφ - S_ysinφ|α>
= <S_x>cosφ - <S_y>sinφ.
Similarly _R<α|S_y|α>_R = <S_y>cosφ + <S_x>sinφ.
The average value of S_z does not change, since it commutes with U(R).  The expectation value of the spin operator S behaves as though it were a classical vector under rotation. 
We have <S_i>_R = ∑_iR_ij<S_j>,
where R is the 3 x 3 rotation matrix for the rotation being considered.  For an arbitrary system we can generalize to
<J_i>_R = ∑_iR_ij<J_j>.
[Remember S is a vector operator.  While the expectation values of the components of S behave as the components of a classical vector under rotation, the components of S itself behave like a classical vector rotated backward, S' = R^-1S.]

How does the state vector of the spin ½ particle behave under rotation?
Let |α> = c₁|+> + c₂|->.
|α>_R = U(R)|α> = exp(-iS_zφ/ħ)|α> = exp(-iφ/2)c₁|+> + exp(iφ/2)c²|->.
For φ = 2π we have  |α>_R = -c₁|+> - c₂|-> = -|α>.
A 360^o rotation does not give us the original ket back.  We need to rotate through 720^o to get back our original state vector.  This is a classically totally unexpected result.

Can it be observed?
The minus sign is a change in the phase of the state vector.  If all state vectors are multiplied by a minus sign there will be no observable effect.  We can only observe changes in relative phase. We must compare a rotated ket to an unrotated ket and look for interference effects.  Assume a spin ½ particle can move from point A to point B along two different path.  Assume that when we observe the particle at point B we do not know which path it actually took to get there. Assume that path 1 does not rotate the state vector and path 2 does rotate the state vector.

Let {|ψ(1)>,|ψ(2)>} be the eigenstates of the observable that determines the path of the particle.  Assume that at point A the state vector is
|α(0)> = 2^(-1/2)(|ψ(1)> + |ψ(2)>).
At point B the state vector is
|α(t)> = 2^(-1/2)U(t,t₀)(|ψ(1)> + |ψ(2)>). 
Assume the evolution operator rotates |ψ(2)> but not |ψ(1)>.  If |ψ(2)> is rotated through 360^o then the state vector at point B is
|α(t)> = 2^(-1/2)(|ψ(1)> - |ψ(2)>).
The probability of finding the particle at point B is
|<r_B|α(t)>|²  = ½|<r_B|ψ(1)> - <r_B|ψ(2)>|².
If without rotation the probability of finding the particle at point B is 1, then with rotation we have destructive interference.

How can we rotate the state vector?
The Hamiltonian of a spin ½ particle in a magnetic field B = Bk is H = ωS_z where ω = -γB is proportional to the magnetic field strength. 
The evolution operator therefore is U(t,0) = exp(-iωS_zt/ħ).
The evolution operator equals the rotation operator with φ = ωt.  This explains spin precession.  In a magnetic field B = Bk we have
<S_x>_t = <S_x>_t=0cos(ωt) - <S_y>_t=0sin(ωt),  <S_y>_t = <S_y>_t=0cos(ωt) + <S_x>_t=0sin(ωt),
<S_z>_t = <S_z>_t=0.

Assume that in a neutron interferometry experiment path 1 goes through a field free region and path 2 goes through a region with a static magnetic field   B = Bk.
Then |α(t)> = 2^(-1/2)(|ψ(1)> + exp(-i(ωT/2)|ψ(2)>).  The intensity at point B is therefore is proportional to C + Dcos(ωT/2).  We can vary the angle φ = ωT by varying the magnetic field strength.  The intensity at point B is predicted to vary sinusoidally with a period 4π/ω.  These predictions have been experimentally verified.

Rotation of two component spinors
We now take into account both the internal and the external degrees of freedom of a spin ½ particle.  Let us rotate the system ccw about the z-axis through an angle φ.  Let |ψ> be the state vector of a spin ½ particle in E = E_r ⊗ E_s before the system is rotated.  |ψ> can be represented by the two component spinor

 .

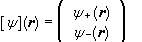After the rotation the state vector is |ψ>_R = U(R)|ψ>, where U(R) = ^rU(R) ⊗ ^sU(R).  U(R) is a mixed operator.
The matrix for ^rU(R) is and the matrix for ^sU(R) is .
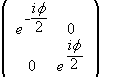We therefore have

.

Group properties of rotations

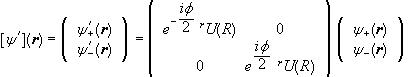
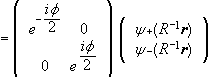How can we characterize a rotation?  We need three real numbers to characterize a general rotation.  We can, for example, specify the direction of the rotation axis (two angles) and the rotation angle.  We can also specify the 3 x 3 rotation matrix R.  R has 9 elements.  R is an orthogonal matrix.  RR^t = R^tR = I.  The orthogonality condition results in a set of 6 independent equations for 9 unknowns.  Therefore R contains 3 independent numbers.

The set of all multiplication operation with orthogonal matrices forms a group.  This group has the name SO(3).  (S stands for special (determinant = 1), O stands for orthogonal, 3 stands for three dimensions.)

We can also characterize a rotation by specifying the 2 x 2 unitary matrix U(R) which is the matrix representations of the rotation operator in E_s.  The most general form of such a rotation matrix is

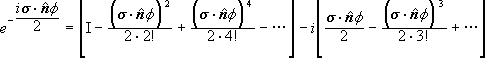
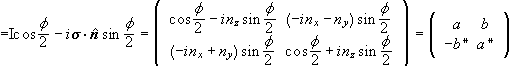
with |a|² + |b|² = 1 and a and b complex numbers.  Again we have 3 independent elements.  The matrices U(R) also form a group.  This group has the name SU(2).  (S stands for special, U stands for unitary, 2 stands for dimensionality 2.)  The groups SO(3) and SU(2) are not isomorphic.  A 2π rotation and a 4π rotation are represented by the same R matrix but by different U(R) matrices.  U(a,b) and U(-a,-b) correspond to the same 3 x 3 rotation matrix in the SO(3) language.  For a given R the corresponding U(R) is double valued.