Assume that the basic laws of physics are the same everywhere.  Then the mechanical properties of a closed system are unchanged by any parallel displacement of the entire system in space.  This is the assumption of the homogeneity of space.

Let T_a describe an operation called a translation.  Every part of the closed system is displaced by the same amount a by this operation.  To every state vector |ψ> before the translation corresponds a state vector |ψ’> after the translation.  Let U(T_a) be the operator that maps the state vector before the translation onto the state vector after the translation, |ψ’> = U(T_a)|ψ>.  Note the difference between the operation and the operator.  If the laws of physics are the same everywhere, then the general formalism describing the properties of the system is invariant under the translation.  In particular we have

|ψ> = c₁|ψ₁> + c₂|ψ₂>  -->  |ψ'> = c₁|ψ₁'> + c₂|ψ₂'>,

i.e. U(T_a) is a linear operator, and <Φ|ψ> = <Φ’|ψ’>,  U^†(T_a)U(T_a) = 1,  U(T_a) is a unitary operator.  We say that translation is a unitaristic operation.

With our assumption of the homogeneity of space, the time evolution is also invariant under translation.
If |ψ(t)> satisfies the Schroedinger equation, so does |ψ’(t)> = U(T_a)|ψ(t)>,
iħ (∂/∂t) U(T_a)|ψ(t)> = HU(T_a)|ψ(t)>.  But
iħ (∂/∂t) U(T_a)|ψ(t)> = iħ U(T_a)(∂/∂t)|ψ(t)> = U(T_a)H|ψ(t)>.
Therefore  HU(T_a)|ψ(t)> = U(T_a)H|ψ(t)>  for any |ψ(t)>,  HU(T_a) = U(T_a)H,  [H,U(T_a)] = 0.

When a = 0, then U(T₀) = I.
Assume that U(T_a) is a differentiable function of a.  Then for a = da
U(T_a) = U(T₀) + ∑_i∂U(T_a)/∂a_i|_a=0da_i = I + ∑_iD_ida_i, with D_i = ∂U(T_a)/∂a_i|_a=0.
I + ∑_iD_ida_i  is the infinitesimal translation operator.

Since UU^† = I, we have (∂U/∂a_i)U^† + U(∂U^†/∂a_i) = 0.  If we evaluate this expression at a = 0 we obtain
(∂U/∂a_i)|_a=0 + (∂U^†/∂a_i)|_a=0 = 0,  D_i + D_i^† = 0.  D_i is anti-Hermitian.
Let P_i = iħD_i, then P_i is Hermitian, it is qualified to describe an observable.

Let us identify P_i.
U(T_a) acting on the state vector |r> yields |r + a>, U^†(T_a) acting on the state vector |r> yields |r - a>.  Therefore
ψ’(r) = <r|U(T_a)|ψ>  =<U^†(T_a)r|ψ> = <r - a|ψ> = ψ(r - a).
We write
U(T_a)ψ(r) = ψ(r - a).
The effect of U(T_a) on a wave function ψ is to produce a wave function ψ’ whose value at r + a is the same as the value of ψ at r.  For an infinitesimal displacement we have
ψ(r - dr) = ψ(r) - ∑_i(∂ψ(r)/∂x_i)dx_i = <r|I + ∑_iD_idx_i|ψ> = ψ(r) + ∑_iD_iψ(r)dx_i.

We therefore have D_iψ(r) = -∂ψ(r))/∂x_i,  P_i = iħD_i = -iħ∂/∂x_i,  i.e. the observables P_i are the components of the momentum of the closed system.
Since [H,U(T_a)] = 0, we have [H,P_i] = 0, P is a constant of motion.  Homogeneity of space implies momentum conservation.

Let us now generalize this result.  If U(λ) is a family of unitary operators depending differentiably on the real parameter λ, with U(0) = I, then  X = iħ(∂U/∂λ)|_λ=0 is a Hermitian operator.  If U(λ) describes the invariance Q_λ, then X is a constant of motion.

Rules:

U(λ + μ)|ψ> = U(λ)U(μ)|ψ>, 
U(λ + dλ)|ψ> = U(λ)U(dλ)|ψ>  = U(λ)(I + (∂U/∂λ)|_λ=0 dλ)|ψ> = U(λ)(I - (i/ħ)X dλ)|ψ>.
U(λ + dλ) - U(λ) = - (i/ħ)X dλ U(λ),  U(λ) = exp(-iXλ/ħ)

X is called the Hermitian generator of the unitary family U(λ).

P is the Hermitian generator of the unitary family of translation operators U(T_a) = exp(-ip∙a/ħ).  The evolution operator is U(t) = exp(-iHt/ħ).  It is of the form U(λ) = = exp(-iXλ/ħ), with X = H and λ = t.  The Hamiltonian is the Hermitian generator of time translation operators.

The rotation operator

Assume that the basic laws of physics are the same in all directions.  Then the mechanical properties of a closed system are unchanged by any rotation of the entire system in space.  This is the assumption of the isotropy of space.  Like translations, rotations are therefore unitaristic operations on the state space of any physical system.  There are unitary operators U(R(n,θ)) representing the effect of a rotation about the n axis through an angle θ.  Let us denote the Hermitian generator of rotation by J.  Then
U(R(n,θ)) = exp(-iJ∙nθ/ħ).

Rotations about different axes do not commute.  As a consequence, the different components of J do not commute. 
We find [J_i,J_j] = iħε_ijkJ_k.  J satisfies the commutation relations for angular momentum.

A rotation is an operation upon 3-dimensional vectors.  The matrix for rotating a system counterclockwise (ccw) through an angle θ about the z-axis is

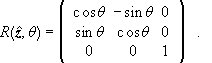
We are describing an active rotation.  The corresponding passive rotation rotates the coordinate system clockwise (cw) an angle θ about the z-axis.  Consider a system without any internal degrees of freedom, for example a spinless particle.  U(R) acting on the state vector |r> yields |(Rr)>, U^†(R) acting on the state vector |r> yields |(R^-1r)>.  Therefore
ψ’(r) = <r|U(R)|ψ>  =<U^†(R)r|ψ> = <(R^-1r)|ψ> = ψ(xcosθ + ysinθ, -xsinsθ + ycosθ, z).
We write ψ’(r) = U(R)ψ(r) = ψ(R^-1r)
The effect of U(R) on a wave function ψ is to produce a new wave function ψ’, whose value at Rr is the same as the value of ψ at r.  For an infinitesimal rotation we have

ψ’(r) = <r|I - iJ∙ndθ/ħ|ψ> = ψ(r) - (iJ∙ndθ/ħ)ψ(r).

But we also have ψ'(r) = ψ(r) - (∂ψ(r)/∂θ)dθ
= ψ(r) - [(∂ψ(r)/∂x)(∂x/∂θ) + (∂ψ(r)/∂y)(∂y/∂θ)]dθ
= ψ(r) - [y(∂ψ(r)/∂x) - x(∂ψ(r)/∂y)]dθ.

Therefore we find J_z = -iħ[x(∂/∂y) - y(∂/∂x)].
Similarly we find J_x and J_y.  We have J = r x p, the classical definition of angular momentum.  We therefore have expressed the rotation operator for a spinless particle in terms of its orbital angular momentum L.
U(R(n,θ)) = exp(-iJ∙nθ/ħ) = exp(-iL∙nθ/ħ),
where L = J = total angular momentum.  In deriving this expression we assumed that ψ(r) completely describes the state of the particle.  This is not true for a particle with spin, a system which has no classical analog.  For such a system we write the rotation operator as U(R(n,θ)) = exp(-iJ∙nθ/ħ), and consider this relation to be the definition of the total angular momentum J of the system.

Rotation of observables

Besides rotating the system itself, we can also rotate the instruments with which we observe it.  We now define the law for the transformation of the observables representing the various measurements that can be made on the system.  Let A be an observable and let A’ be its transform in the rotation, i.e. A describes what is measured with a certain apparatus, and A’ describes what is measured after the apparatus has been rotated.  The average value of A in the state |ψ> must equal the average value of A’ in |ψ’>.  (Isotropy of space implies that if the system and the observer are rotated together, the physical predictions remain unchanged.)
<ψ|A|ψ> = <ψ'|A'|ψ'> = <Uψ|A'|Uψ> = <ψ|U^†A'U|ψ>  for all |ψ>.
Therefore  A = U^†(R)A'U(R),  A' = U(R)A'U^†(R).

Scalar observables
An observable A is a scalar observable if
A’ = A, U(R)AU^†(R) = A, U(R)A = AU(R), [U(R),A] = 0, or
[I - iJ∙ndθ/ħ,A] = 0,  [J∙n,A] = 0,  [J,A] = 0,
i.e. if A commutes with all components of J.  An example of a scalar observable is J².

Vector observables
A vector observable V is a set of three observables, V_x, V_y, V_z, which transform under a rotation R like V’ = R^-1V. 
For an infinitesimal ccw rotation R about the z-axis we have V’_x = cosθ V_x + sinθ V_y = V_x + dθ V_y. 
We have
V’_x = UV_xU^† = (I - iJ_zdθ/ħ) V_x (I + iJ_zdθ/ħ) = V_x - (idθ/ħ)J_zV_x + (idθ/ħ)V_xJ_z.
We therefore have V_y = (i/ħ)[V_x,J_z],  or  [V_x,J_z] = -iħV_y.
Similarly we show  [V_y,J_z] = iħV_x.
This leads to an alternate definition of a vector observable V.
[V_i,J_j] = -iħε_ijkV_k.
An example of a vector observable is J itself.

Problem:
Conservation laws are intrinsically related to the invariance of a physical system.  Show classically and quantum mechanically that the conservation of angular momentum is a consequence of isotropy of space.

Solution:
Properties of an isolated physical system do not vary when it is rotated as a whole in any manner in space.  This is the assumption of isotropy of space.  Assume a system is rotated about the u axis by an infinitesimal amount dα.
(i)  Classically, the equations of motion must be invariant under the rotation.  The equations of motion can be derived from the Lagrangian L(r,v,t).  Therefore the Lagrangian must remain unchanged by the rotation. 
Under the rotation r --> r + dα u x r,   v --> v + dα u x v.

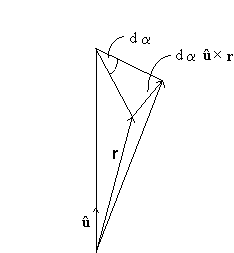
Therefore δr = dα u x r,   δv = dα u x v.
Isotropy of space implies that
 
Using the definition ∂L/∂v_n = p_n we obtain from
.
We therefore have, (using a × (b x c) = b ×(c x a) = c × (a x b)),

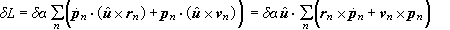
δα u ∙ (d/dt)∑_n(r_n x p_n) = 0 for all u.
This implies (d/dt)∑_n(r_n x p_n) = 0,  angular momentum is conserved.

(ii) Quantum mechanically, we consider an isolated system in the state |ψ(t)>.  After an arbitrary rotation the state of the system becomes |ψ’(t)> = U(R)|ψ(t)>.  Rotational invariance implies that the time evolution is not affected by the rotation, i.e. [H,U(R)] = 0.
Therefore [H,(I - iJ∙udα/ħ)] = 0,  [H,J∙u] = 0,   [H,J] = 0.
H commutes with all components of J, therefore J is a constant of motion.

Rotational invariance implies that the total angular momentum of an isolated physical system is a constant of motion.  We therefore always can find common eigenstates of H, J², and J_z.  We denote the common eigenbasis by {|k,j,m>}.  Using this standard basis we find that the matrix elements of any scalar operator are non zero only between states with the same values of j and m.
Let A be a scalar observable, [A,U(R)] = 0, [A,J²] = 0, [A,J_z] = 0.  Then

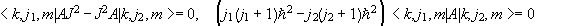
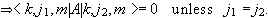
Similarly

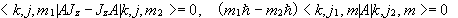
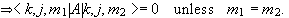
Moreover, the matrix elements of a scalar observable are independent of m.

.
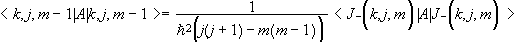
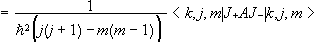
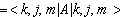