We study "square" potentials, or piece-wise constant potentials, because they may crudely approximate real potentials.  Let us concentrate on one-dimensional "square" potentials.  Assume U(x) = U = constant in certain regions of space.  In such regions the time-independent Schroedinger equation,  HΦ(x) = EΦ(x,) can be written as

∂²Φ(x)/∂x² + (2m(E - U)/ħ²)Φ(x) = 0.

We find the eigenfunction of H by solving HΦ_E(x) = EΦ_E(x).
We can solve this equation in regions of piecewise constant potentials.

Let E > U:
Then ∂²Φ(x)/∂x² + k²Φ(x) = 0,   k² = 2m(E - U)/ħ².
The most general solution is Φ(x)  = Ae^ikx + A'e^-ikx, with A and A’ complex constants.

Let E < U:
Then ∂²Φ(x)/∂x² - ρ²Φ(x) = 0,   ρ² = 2m(U - E)/ħ².
The most general solution is Φ(x) = Be^iρx + B'e^-iρx, with B and B’ complex constants.
Note: A solution exists in the classically forbidden region.

Let E = U:
∂²Φ(x)/∂x² = 0
The most general solution is  Φ(x) = Cx + C', with C and C’ complex constants.

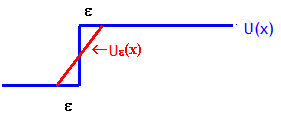
Approximate U(x) by U_ε(x), which is equal to U(x) everywhere except in a small region x₁ ± ε, where it does not have the step but varies continuously.  We can write the Schroedinger equation as a difference equation,
∂Φ_ε(x₁ + ε)/∂x + ∂Φ_ε(x₁ - ε)/∂x = (2m/ħ²)∫_x1-ε^x1+ε (U_ε(x) - E) Φ(x) dx
As ε --> 0, U_ε(x) remains finite, and therefore the integral remains finite and decreases as ε decreases.  For ε = 0 the integral is zero.  Therefore ∂Φ_ε/∂x|_ε-->0 is continuous. 
At a finite step the boundary conditions are that Φ(x) and ∂Φ(x)/∂x are continuous.

(b)  Assume U(x) does not remain finite on one side of the step. 
Approximate U(x) by U_ε(x) such that U_ε(x) has a step ∆U over a small interval 2ε = 2c/∆U. 
As ε --> 0, ∆U --> ∞, and  ∫_x1-ε^x1+ε (U_ε(x) - E) Φ(x) dx  ≈ Φ(x₁)[c - 2εE]  --> cΦ(x₁).

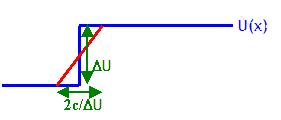
At an infinite step ∂Φ_ε/∂x|_ε-->0 is discontinuous, but it has a finite discontinuity.  Therefore Φ(x) remains continuous as  ε --> 0.
In a region of finite width ∆x, where |U| is infinite, the wave function must be zero everywhere.  Since the wave function is continuous, it also must be zero also at the boundary in the adjacent region.  If |U| is infinite in a region with width ∆x = 0 (a δ-function, for example), the wave function can be finite there.  It will have the same value at the boundaries of the two adjacent regions and its derivative with respect to x will be discontinuous.