Problem:

Consider the square potential well shown in the figure below.

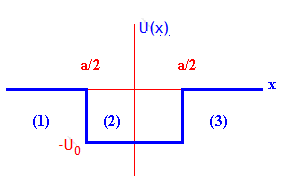
(a)  Find the most general solution Φ(x) of the eigenvalue equation HΦ(x) = EΦ(x), (E < 0), in regions 1, 2, and 3 and apply boundary conditions.
(b)  Solve the equation that results from part (a) graphically, and find the conditions under which even and odd solutions exist.

Solution:

• Concepts:
  This is a "square potential" problem.  We solve HΦ(x) = EΦ(x) in regions where U(x) is constant and apply boundary conditions.
• Reasoning:
  We are given a piecewise constant potential and are asked to find bound-state solutions.
• Details of the calculation:
  Let -U₀ < E < 0.  The wave function must remain finite at x = ± ∞.  We therefore have:
  Φ₁(x) = B₁e^iρx,   Φ₂(x) = A₂e^ikx + A₂'e^-ikx,  Φ₃(x) = B₃'e^-iρx,
  with k² = (2m/ħ²)(E + U₀) and ρ² = (2m/ħ²)(-E).
  Φ and ∂Φ/∂x  are continuous at x = ± a/2  This implies:
  B₁e^-ρa/2 = A₂e^-ika/2 + A₂'e^ika/2,  B₃'e^-ρa/2 = A₂e^ika/2 + A₂'e^-ika/2.
  ρB₁e^-ρa/2 = ikA₂e^-ika/2 - ikA₂'e^ika/2,  -ρB₃'e^-ρa/2 = ikA₂e^ika/2 - ikA₂'e^-ika/2.
  Solving for A₂ and A₂^’ in terms of B₁ we obtain
  A₂ = e^{(-ρ + ik)(a/2)}(ρ + ik)/(2ik)B₁,  -A₂' = e^{-(ρ + ik)(a/2)}(ρ - ik)/(2ik)B₁.
  Solving for A₂ and A₂^’ in terms of B₃^’ we obtain
  -A₂ = e^{-(ρ + ik)(a/2)}(ρ - ik)/(2ik)B₃',  A₂' = e^{(-ρ + ik)(a/2)}(ρ + ik)/(2ik)B₃'.
  This yields two equations for B₃^’ in terms of B₁,
  -B₃' = [(ρ + ik)/(ρ - ik)]e^ikaB₁  and  -B₃' = [(ρ - ik)/(ρ + ik)]e^-ikaB₁,
  which can only simultaneously be satisfied if
  [(ρ - ik)/(ρ + ik)]² = e^2ika.
  There are two possible solutions.
  
  Solution 1:
  [(ρ - ik)/(ρ + ik)] = -e^ika
  But we also have
  [(ρ - ik)/(ρ + ik)] = [(ρ² + k²)^1/2e^-iθ/(ρ² + k²)^1/2e^iθ] = e^-i2θ, with cotθ = ρ/k.
  This implies
  e^-i2θ = -e^ika,  -2θ = ka - π,  cotθ = cot(π/2 - ka/2) = tan(ka/2) = ρ/k.
  How do you solve an equation like this for k?
  We can try a graphical solution. 
  Define  k₀² = 2mU₀/ħ² = k² + ρ².
  Then 1/cos²(ka/2) = 1 + tan²(ka/2) = (k² + ρ²)/k² = k₀²/k²,
  or |cos(ka/2)| = k/k₀  for all k for which tan(ka/2) ≥ 0.
  Note: We changed from a tangent to a cosine function for easier graphing.
  
  
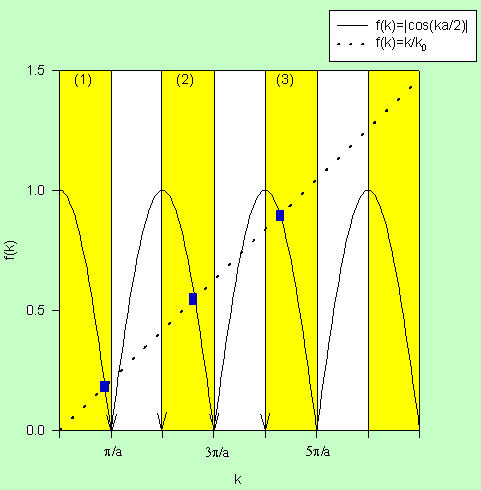
  In regions (1), (2), (3,) ...  tan(ka/2) ≥ 0.  Three solutions exist for the given k₀ in the graph.  As we increase k₀ more solutions become possible.  For every k₀ at least one solution is possible.  There exists at least one bound state.  But we have not yet found the complete set of solutions.
  
  Solution 2:
  [(ρ - ik)/(ρ + ik)] = +e^ika
  This implies e^-i2θ = e^ika,  -2θ = ka,  cotθ = cot(-ka/2) = -cot(ka/2) = ρ/k.
  Then 1/sin²(ka/2) = 1 + cot²(ka/2) = (k² + ρ²)/k² = k₀²/k²,
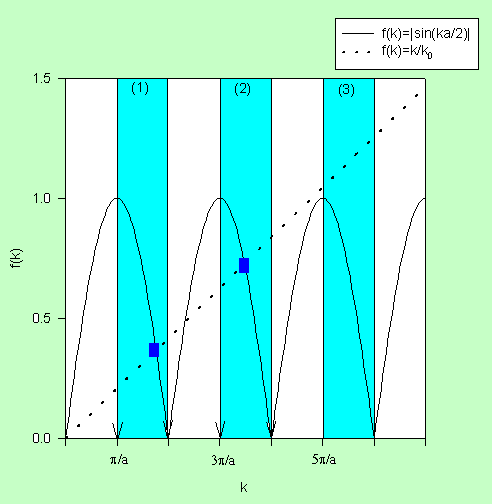
  or |sin(ka/2)| = k/k₀ for all k for which cot(ka/2) ≤ 0. 
  We construct a similar graph to get more solutions.
  
  
   

  After we have found our solutions for k we can substitute  [(ρ - ik)/(ρ + ik)] = ±e^ika  back into the equations giving the relations between the A’s and B’s.  We find:
  if [(ρ - ik)/(ρ + ik)] = -e^ika  then A₂ = A₂', B₁ = B₃', Φ(-x) = Φ(x), the solutions are even;
  if  [(ρ - ik)/(ρ + ik)] = +e^ika  then A₂ = -A₂', B₁ = -B₃', Φ(-x) = -Φ(x), the solutions are odd.

  For k₀ ≤ π/a only one (even) solution exists.
  If π/a ≤ k₀ ≤ 2π/a  the first odd solution becomes possible. 
  If k₀ is very large, then the slope of the straight line is very small and solutions appear near every k = nπ/a (n = integer).  Consequently 
  E_n = n²π²ħ²/(2ma²) - U₀.
  These are the energy levels of the infinite square well.

We can solve this equation in regions of piecewise constant potentials.

• Regions that do not contain a well
  • There exists an eigenfunction for every E > U_min.  These eigenfunctions, however, are plane waves and are not square integrable.  They cannot represent a single particle, but can represent a constant flux of particles.  We calculate transmission and reflection coefficients by comparing fluxes. 
    (Flux = k|Φ(x)|².)
     
• Regions that do contain a well
  • There exists an eigenfunction for every E > E_rim.  These eigenfunctions are not square integrable.
  • For E < E_rim eigenfunctions exist only for selected eigenvalues.  We can solve for the bound states in a square-well potential using a graphical solution.

Confinement leads to energy quantization.