

Let us consider the behavior of tan energy eigenfunction Φ(x) at a potential
step.
Φ(x) is a solution of the differential equation
∂2Φ(x)/∂x2 + (2m(E -
U)/ħ2)Φ(x) = 0.
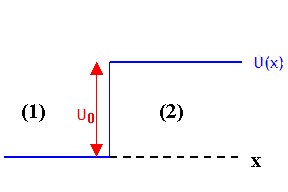
(a) Assume E > U0.
The most general solutions in regions 1, and 2 are
Φ1(x) = A1exp(ik1x) + A1'exp(-ik1x),
Φ2(x) = A2exp(ik2x) + A2'exp(-ik2x),
Here k12 = (2m/ħ2)E and k22
= (2m/ħ2)(E - U0).
Φ is continuous at x = 0.
Therefore A1 + A1' = A2 + A2' .
(∂/∂x)Φ(x) is continuous at x = 0.
Therefore ik1A1 - ik1A1' = ik2A2
- ik2A2' .
We have two equations and four unknowns. No unique solution exists.
Let us limit
ourselves to particles approaching from the left being transmitted or reflected at the
barrier. Assume A2' = 0.
We can then solve for A1'/A1 and A2/A1.
We find
A1'/A1 = (k1 - k2)/(k1
+ k2), A2/A1 = 2k1/(k1
+ k2) .
The ratios are real and positive, there is no
phase shift upon reflection and transmission.
Probability of Reflection (R) and Transmission (T):
Our solutions in regions 1 and 2 are plane wave solutions. They are not square-integrable,
and a proper normalization is not possible. Plane wave solutions are useful in describing
steady streams of particles. To evaluate the probability of reflection and transmission
for such beams, we compare the reflected and transmitted
flux with the incident flux.
Let P(x) be the probability density at x, let x0 be some
point in region 1, and let x0’ be some point in region
2. We then have
incident flux ∝ v1Pi(x0)
reflected flux ∝ v1Pr(x0)
transmitted flux
∝ v2Pt(x0')
The reflectance R is R = (v1Pr(x0))/(v1Pi(x0))
= |A1'/A1|2,
and the transmittance T is T = (v2Pt(x0'))/(v1Pi(x0))
= (k2/k1)|A2/A1|2,
We have R = 1 - 4k1k2/(k1 + k2)2,
T = 4k1k2/(k1 + k2)2, R + T =
1.
Classically the probability of reflection is zero.
In Quantum Mechanics
R --> 0, T --> 1 if E >> U0 and k2
--> k1.
(b) Assume E < U0.
Let k12
= (2m/ħ2)E and ρ22
= (2m/ħ2)(U - E).
Then Φ1(x)
= A1exp(ik1x) + A1'exp(-ik1x)
and Φ2(x)
= B2exp(ρ2x) + B2'exp(-ρ2x)
are the most general solutions. We need B2 = 0 for the solution to
remain finite at x --> ∞.
Φ is continuous at x = 0.
Therefore A1 + A1' = B2' .
(∂/∂x)Φ(x) is continuous at x = 0.
Therefore ik1A1 - ik1A1' =
-ρ2B2'.
We find
A1'/A1 = (k1 -
iρ2)/(k1
+ iρ2),
B2/A1 = 2k1/(k1 +
iρ2) .
The ratios are complex, a
phase shift appears upon reflection.
We compute R by comparing the
incident and the reflected flux, R = |A1'/A1|2
= 1.
Therefore T = 0, there is no transmitted flux.
Note: As U0 --> ∞,
ρ2 --> ∞. Then A1'/A1
--> -1, B2'/A1 --> 0,
we have a phase shift of 1800.
If U0 = ∞ then A1' = -A1,
B'2 = 0, Φ2(x) = 0, Φ(x) is
continuous at x = 0 since Φ(0) = 0, but
∂Φ/∂x is not continuous.
We have Φ1(x)
= 2iA1sin(k1x), ∂Φ1/∂x
= 2iA1k1cos(k1x), ∂Φ1/∂x|x=0
≠ 0.