Consider the 1-dimensional, quantum mechanical system consisting of a single structure-less particle.
How well do the classical equations of motion describe the motion of this particle?

We have Ehrenfest’s theorem, d<X>/dt = <P>/m,  d<P>/dt = -<dU(x)/dx>.
The classical equations of motion work best when the potential varies slowly with distance.

Assume the potential is a slowly varying function of distance, U = U(x), independent of time. 
Then solutions of the form Ψ_E(x,t) = Φ_E(x) exp(-iEt/ħ) can be found. 
Φ_E(x) is a solution of
∂²Φ(x)/∂x² + k²(x) Φ(x) = 0,   E > U,
or 
∂²Φ(x)/∂x² - ρ²(x)Φ(x) = 0,   E < U,
where k²(x) = (2m(E - U(x))/ħ²),  ρ²(x) = (2m(U(x) - E)/ħ²).

Let us try a solution of the form Φ(x)  = A exp((i/ħ)S(x)).
[Any complex function of x can be written as Φ(x)  = A(x) exp(i S(x)/ħ).]  
Substituting this solution into the time-independent Schroedinger equation we obtain
iħd²S/dx² - (dS/dx)² + ħ²k²(x) = 0,  or  iħd²S/dx² - (dS/dx)² - ħ²ρ²(x) = 0.
(For a potential square well S(x) = ±ħkx inside the well and ±iħρx outside the well.)

Assume that ħ can, in some sense, be regarded as a small quantity and that S(x) can be expanded in powers of ħ, S(x) = S₀(x) + ħS₁(x) + ... .
Then
iħd[dS₀/dx + ħdS₁/dx + ... ]/dx - [dS₀/dx + ħdS₁/dx + ... ]² + ħ²k²(x) = 0,   (E > U(x)).
We assume that |dS₀/dx| >> |ħdS₁/dx| and collect terms with equal powers of ħ. 
[Note: ħ²k² is zeroth order in ħ, since k(x) = (2m(E - U(x))/ħ²)^1/2.]

[dS₀/dx]² + ħ²k²(x) = 0  -->  S₀ = ±∫^x ħk(x') dx'.
id²S₀/dx²  - 2(dS₀/dx)(dS₁/dx) = 0 --> S₁ = ½i ln(k(x)).
We have used 
id[S₀/dx]/dx  = 2(dS₀/dx)(dS₁/dx),
idk/dx = 2k dS₁/dx,  dS₁ = (i/2)dk/dk.
Therefore Φ(x)  = A k(x)^-1/2 exp(±i∫^x k(x') dx'.
In the classically allowed region S₀ = ±∫^x ħk(x') dx' counts the oscillations of the wave function.  An increase of 2πħ corresponds to an additional phase of 2π.
Similarly, in regions where E < U(x) we have
Φ(x)  = A ρ(x)^-1/2 exp(±∫^x ρ(x') dx'.
This is the WKB (Wentzel, Kramers, Brillouin) approximation.

When is the  WKB approximation valid?

For our first order expansion to be accurate we need that the magnitude of higher order terms decreases rapidly. 
We need  |dS₀/dx| >> |ħdS₁/dx| or k >> |(2k)^-1dk/dx|.
The local deBroglie wavelength is λ = 2π/k. 
Therefore we need |(λ /4π)(dλ/dx)| << λ,  i.e. the change in λ over a distance λ /4π is small compared to λ .
This holds when the potential varies slowly and the momentum of the particle is nearly constant over several wavelength.
Near the classical turning points the WKB solutions become invalid, because k goes to zero here.  We have to find a way to connect an oscillating solution to an exponential solution across a turning point if we want to solve barrier penetration problems or find bound states.

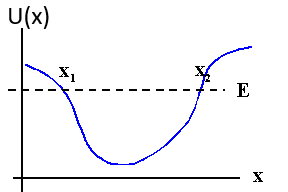
For x < x₁ the wave function is of the form 
Φ₁(x)  = A₁ ρ^-1/2 exp(+∫^x ρ(x') dx'.
For x > x₂ the wave function is of the form 
Φ₃(x)  = A₃ ρ^-1/2 exp(-∫^x ρ(x') dx'. 
In the region between x₁ and x₂ it is of the form
Φ₂(x)  = A₂ k^-1/2 exp(+i∫^x k(x') dx' + A₂' k^-1/2 exp(-i∫^x k(x') dx'.
At x = x₁ and x = x₂ the wave function Φ and its derivative have to be continuous. 
How do we apply these boundary conditions?
Near x₁ and x₂ we expand the potential in a Taylor series expansion in x and neglect all terms of order higher than 1.
Near x₁ we have U(x) = E - K₁(x - x₁), and near x₂ we have U(x) = E - K₂(x + x₂), with K₁ and K₂ positive constants.
In the neighborhood of x₁ the time-independent Schroedinger equation then becomes
∂²Φ(x)/∂x² +  (2mK₁/ħ²)(x - x₁) Φ(x) = 0,
and in the neighborhood of x₂ the time-independent Schroedinger equation becomes
∂²Φ(x)/∂x² -  (2mK₂/ħ²)(x - x₂) Φ(x) = 0.

Let us define  z = -(2mK₁/ħ²)^1/3(x - x₁).
Then we obtain ∂²Φ/∂z² -  zΦ = 0 near x₁.
The solutions of this equation which vanish asymptotically as  z --> ∞ or x --> ∞  are the Airy functions.  They are defined through
Ai(z) = π^-1∫₀^∞ cos(s³/3 + sz)ds
which for large |z| has the asymptotic form
Ai(z) ≈ (2 √π z^1/4)^-1 exp(-2z^3/2/3),  (z > 0),
and
Ai(z) = (√π (-z)^1/4)^-1 sin(2(-z)^3/2/3 + π/4),  (z < 0).
If the energy is high enough the linear approximation to the potential remains valid over many wavelength.
The Airy functions can therefore be the connecting wave functions through the turning point at x₁.

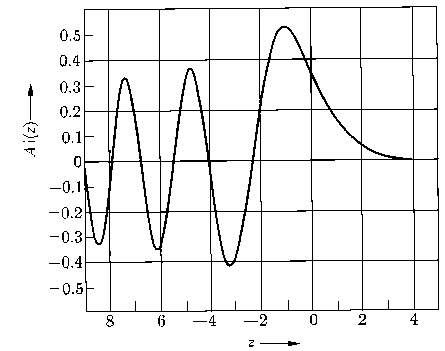
If we define z = (2mK₂/ħ²)^1/3(x - x₂) then we find ∂²Φ/∂z² -  zΦ = 0 near x = x₂ and the Airy functions can also be the connecting wave functions through the turning point at x₂. 

In the neighborhood of x₁ we have k² = -ρ² =  (2mK₁/ħ²)^1/3(x - x₁) = -(2mK₁/ħ²)^2/3z
Therefore ∫_x1^x ρ dx' = (2mK₁/ħ²)^1/3∫_x1^x √z dx' = -∫₀^z √z' dz' = -2z^3/2/3.
Similarly ∫_x1^x k dx' = (2mK₁/ħ²)^1/3∫_x1^x √(-z) dx' = -∫₀^z √(-z') dz' = -2(-z)^3/2/3.
By comparing this with the asymptotic forms of the Airy functions we note that 
Φ₁(x)  = A₁ ρ^-1/2 exp(+∫_x1^x ρ(x') dx'   (x < x₁)
must continue on the right side as 
Φ₂(x)  = 2A₁ k^-1/2 sin(∫_x1^x kdx'  +  π/4)    (x > x₁).

In the neighborhood of x₂ we similarly find that 
Φ₃(x)  = A₃ ρ^-1/2 exp(-∫_x2^x ρ(x') dx'   (x > x₂)
must continue in region 2 as   
Φ₂(x)  = 2A₃ k^-1/2 sin(∫_x^x2 (kdx'  +  π/4)   (x < x₂). 
Both expressions for Φ₂(x) are approximations to the same eigenfunction.  We therefore need
2A₁ k^-1/2 sin(∫_x1^x (kdx ' +  π/4) =  2A₃ k^-1/2 sin(∫_x^x2 (kdx' +  π/4).
Writing ∫_x1^{x =} ∫_x1^x2 - ∫_x^x2, we require 
sin[∫_x1^x2 k dx' -  ∫_x^x2 kdx' + π/4)] = (A₃/A₁)sin[∫_x^x2 k dx' + π/4].
This condition is only satisfied if  ∫_x1^x2 k dx =  (n + ½)π, n = integer.
This can be rewritten as  ∫_x1^x2 p dx =  (n + ½)h/2,  or  ∫_cylce p dx  = (n + ½)h.
Here ∫_cylce denote an integral over one complete cycle of the classical motion.
The WKB method for bound states therefore leads to the Wilson- Sommerfeld quantization rule except that n is replaced by (n + ½). 
It leads to a quantization of the classical action J = ∫_cylce p dq.

If we let n = 0, 1, 2, ..., then n counts the number of zero of the wave function in the well.  We may also let n = 1, 2, 3, ... , and write ∫_x1^x2 k dx =  (n - ½)π.  Then n counts the number of anti-nodes of the wave function in the well.  If our potential well has one or two vertical walls, the results of the WKB approximation differ only in the number that is subtracted from n = 1, 2, 3, ... , respectively.
For one vertical wall we have ∫_x1^x2 k dx =  (n - ¼)π and for two vertical walls we have ∫_x1^x2 k dx =  nπ.
Since the WKB approximation works best for large n in the semi-classical regime, this distinction is more in appearance than in substance.

Problem:

Use the WKB approximation to derive the energy levels of a particle of mass m confined to the one-dimensional potential U(x) = F|x|.

Solution:

• Concepts:
  The WKB approximation
• Reasoning:
  We are instructed to use the WKB approximation.  The WKB approximation requires that  ∫_xmin^xmax pdx = (n + ½)(h/2) or ∫_cylce p dx  = ∫_cylce ħk dx  = (n + ½)h, n = 0, 1, 2, ... .   Here ∫_cylce denotes an integral over one complete cycle of the classical motion and  k² = (2m/ħ²)(E - U(x)).
• Details of the calculation:
  For stationary bound states we want ∫_xmin^xmax pdx = (n + ½)πħ, n = 0, 1, 2, ... .
  In our problem k²(x) = 2m(E - F|x|)/ħ².
  We need  (2m)^1/2∫_xmin^xmax dx (E - F|x|)^1/2 = 2(2m)^1/2∫_x0^xmax dx (E - Fx)^1/2 = (n + ½)πħ.
  Here Fx_max = E,  x_max = E/F.
  Therefore
  -2(2m)^1/2 (2/(3F)) (E - F|x|)^3/2|_x0^xmax =  4(2m)^1/2/(3F))E^3/2  = (n + ½)πħ.
  E = [3π(n + ½)/(4√2)]^2/3(Fħ)^2/3/m^1/3.
  For n = 1 (the first excited state), for example, we have
  E = 1.84 (Fħ)^2/3/m^1/3.