Assume {|u_i>} and {|t_i>} are orthonormal bases and the operator U changes one basis into the other, i.e. U|u_i> = |t_i> for all basis vectors.  Then the operator U is a unitary operator.
Proof:
For every basis vector
<u_i|U^† = <t_i|,  U^†U|u_i> = U^†|t_i> = ∑_j|u_j><u_j|U^†|t_i> = ∑_j|u_j><t_j|t_i> = |u_i>
-->  U^†U = I.
Similarly,
UU^†|u_i> = U∑_j|u_j><u_j|U^†|u_i> = ∑_jU|u_j><t_j|u_i> = ∑_j|t_j><t_j|u_i> = |u_i>
==>  UU^† = I.

Every unitary transformation transforms one basis into another.
Proof:
Assume that U is unitary and that {|u_i>} is a basis and that U|u_i> = |t_i>.  Then
<t_i|t_j> = <u_i|U^†U|u_j> = <u_i|u_j> = δ_ij.
The vectors {|t_i>} are orthonormal. 
Are they a basis? 
We have to show that every |ψ> can be expanded in terms of the {|t_i>}.  Let |ψ> be an arbitrary vector in a vector space E.
U^†|ψ> ∉ E, therefore  U^†|ψ> = ∑_id_i|u_i>.
It follows that  UU^†|ψ> = ∑_id_iU|u_i> = ∑_id_i|t_i>.
or  |ψ> = ∑_id_i|t_i>.
Therefore {|t_i>} is a basis.
Changing a basis is therefore called a unitary transformation.
A unitary transformation is equivalent to a change of basis.

Let U be the unitary transformation transforming {|u_i>} into {|t_i>}.  The matrix elements of U in the first basis are <u_i|U|u_j> = <u_i|t_j> = U_ij. 
|ψ> = ∑_jd_j|t_j> = ∑_j<t_j|ψ>|t_j>  and  |ψ> = ∑_ja_j|u_j> = ∑_j<u_j|ψ>|u_j>.
We find the components of a vector |ψ> in the second basis in terms of the components in the first basis using
<t_i|ψ> = ∑_j<t_i|u_j><u_j|ψ> = ∑_jU_ji*<u_j|ψ> = ∑_jU^†_ij<u_j|ψ>.
We have
d_i = <t_i|ψ> = ∑_jU^†_ij<u_j|ψ> =  ∑_jU^†_ija_j.
Similarly,  a_i =  ∑_jU_ijd_j.

Example:

• Rotation of the coordinate system through an angle θ is a change of basis, i.e. a unitary transformation.  
  The basis vectors of the first basis are {i, j} = {|x_i>}.
  The basis vectors of the second basis are  {i', j'} = {|x_i'>}.
  We have U|x_i> = |x_i'>,  U_ij = <x_i|U|x_j> = <x_i|x_j'>.
  U₁₁ = <x₁|x₁'> = cosθ,  U₁₂ = <x₁|x₂'> = cos(90^o + θ) = -sinθ,
  U₂₁ = <x₂|x₁'> = cos(90^o - θ) = sinθ,  U₂₂ = <x₂|x₂'> = cosθ.
  The components of |A> in the {|x_i’>} basis are given in terms of the components of |A> in the {|x_i>} basis.
  A_i' = ∑_jU^†_ijA_j,
  or  .
  What happens to the components of a second vector |B> = Ω|A>?
  Ω|A> = |B>, or  . 
  In terms of the components in the {|x_i>} basis.
  We can write
  
  The matrix of Ω in the {|x_i’>} basis is equal to the matrix of U^†ΩU in the {|x_i>} basis.

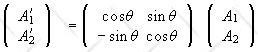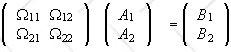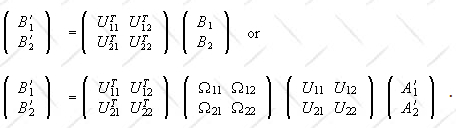
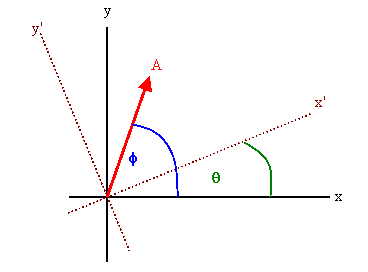
Let Ω be the projector onto the x axis in the {|x_i>} basis.  The matrix of Ω in the {|x_i>} basis is
Ω_ij = 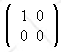, and we have
.

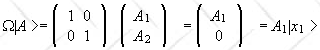The matrix of Ω in the {|x_i’>} basis is
,
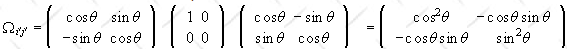and we have
 
exactly the same as in the {|x_i>} basis.

The operator Ω does something different to the {|x_i’>} basis vectors then to the {|x_i>} basis vectors.  Let Ω’ be the operator that does to the new basis vectors what Ω does to the old basis vectors.

• If Ω is the projector on the x axis, then Ω’ is the projector on the x’ axis.

The matrix elements of Ω’ in the {|x_i’>} basis are the same as the matrix elements of Ω in the {|x_i>} basis.
Ω’_i’j’  = Ω_ij.
But
Ω’_i’j’  = (U^†Ω’U)_ij  and therefore Ω_ij = (U^†Ω’U)_ij  or (UΩU^†)_ij = Ω'_ij.

We distinguish between active and passive unitary transformations.
Active:  Change all vectors |ψ> to U^†|ψ>.
Passive:  Change the basis from {|u_i>} to {U|u_i>}.

Active:  The operator Ω still does the same thing to all basis vectors.  But if |Φ> = Ω|ψ> then |Φ’> ≠ Ω|ψ’>.   We have |Φ’> = U^†|Φ> = U^†Ω|ψ> = U^†ΩU|ψ’>.  In our example the rotated vector has a different projection onto the x axis.
Passive:  The operator  Ω changes into Ω’, which does the same thing to the new basis vectors as Ω does to the old basis vectors.  Ω’ = UΩU^†.  In our example the projector onto the x axis becomes the projector onto the x’ axis.

• (a)  Active transformation:  Rotate A clockwise. A' = U^†A.
  .
  Project A onto the x-axis.
  The projector onto the x axis is ΩA' = (cosθ A₁ + sinθ A₂).
  
  (b)  Passive Transformation:  Rotate the coordinate system counterclockwise.
  Do not change A.  Project A onto the x'-axis.
  Change Ω into Ω’ = UΩU^†.  The projection onto the x’ axis is UΩU^†A.
  In matrix notation we find the matrix elements of U Ω U^† and the components of A in some basis.  Let us choose the new basis. 
  Then  UΩU^† = .
  The matrix of UΩU^† in the new basis is the same as the matrix of Ω in the old basis.
  
  In the new basis  .
  
  Therefore UΩU^†A = (cosθ A₁ + sinθ A₂).  The results of the active and the passive transformation are the same.

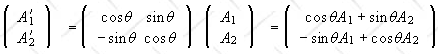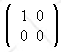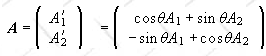We will soon show that the operator describing the evolution of a physical system is a unitary operator.  Therefore the evolution is a unitary transformation.
There are two ways of looking at a unitary transformation.  The Schroedinger picture of quantum mechanics treats it as an active transformation.  The state vector changes with time, the operator does not change unless it contains time explicitly.  The wave function evolves in time.  The Schroedinger equation describes this evolution in a particular representation.
The Heisenberg picture of quantum mechanics treats the unitary transformation as a passive transformation.  The state vector is fixed, the operators change with time.  Both approaches yield the same predictions.