An operator operating on the elements of the vector space V has certain kets, called eigenkets, on which its action is simply that of rescaling.  Ω|V> = ω|V>.  |V> is an eigenket (eigenvector) of Ω, ω is the corresponding eigenvalue.

• If we are solving HΦ  =  EΦ  or  -(ħ²/(2m))∂²Φ(x)/∂x² + U(x)Φ(x)  = EΦ(x),
  then we are solving for the eigenvectors Φ(x) ∈ V = L_x²  of 
  H = -(ħ²/(2m))∂²/∂x² + U(x)),
  and for the corresponding eigenvalues E.

If |V> is an eigenvector, so is a|V>.  The eigenvectors are only fixed to an overall scale factor.  If we require that <V|V> = 1, the ambiguity is partially removed, a phase factor e^iβ is still arbitrary.

•   I|V> = |V>.  Every vector is an eigenvector of the identity operator with eigenvalue 1.
•   P_V = |V><V|.  If <V|V> = 1, then P_V is the projector into the subspace spanned by |V>.
  Let P_V|V’> = a|V’> = |V><V|V’>.
  <V|V’> is a number.
  If <V|V’> ≠ 0 then we need |V’> = b|V> for |V‘> to be an eigenvector.  Then a = 1.
  If <V|V’> = 0 then a = 0.
  The eigenvalues of P_V are either 0 or 1. The eigenvectors of P_V are either perpendicular or parallel to |V> with eigenvalues 0 and 1 respectively.

How do we find the eigenvalues and eigenvectors of an arbitrary linear operator Ω?
Ω|ψ> = ω|ψ>,   (Ω - ω I)|ψ> = 0.
We can transform this equation into a matrix equation by choosing a basis {|u_i>} such that
|ψ> =  ∑_ic_i|u_i>.  Then  ∑_j(Ω_ij - ωδ_ij)c_j = 0.
This matrix equation has a nontrivial solution only if det(Ω - ω I) = 0.  (For a trivial solution all c_j are zero.)
 
This is the characteristic equation.
The determinant is

Here ε_ijk = 1  for even permutations, ε_ijk = -1  for odd permutations, and ε_ijk = 0  for repeating indices.

Our characteristic equation therefore is a polynomial of order N in ω, where N is the dimension of the vector space.  It has N roots.  These roots can be real or complex, distinct or identical.  These N roots are the eigenvalues.  They are found in a particular basis, but are independent of the choice of basis.  If the vector space V is defined over the space of complex numbers, then each linear operator Ω has at least one eigenvalue.  The characteristic equation has at least one root.

• Let Ω be the operator rotating the vector A clockwise through an angle θ in two dimensions.  The matrix of Ω in the {i, j} basis is
   .
  The eigenvalues are found from det(Ω - ω I) = 0.
  or (cosθ - ω)² + sin²θ = 0.
  We have ω² - 2ωcosθ + 1 = 0, ω = cosθ ± (cos²θ - 1)^1/2 = cosθ ± i sinθ.
  For sinθ ≠ 0 no real, but two complex solutions exist.

How do we find the eigenvectors associated with the eigenvalues?
Assume one of the eigenvalues is ω. 
We have to solve the system of N equations,  ∑_j(Ω_ij - ωδ_ij)c_j = 0,  (i = 1 to N) for the unknowns c_j.  If Ω is a linear operator and |ψ> is an eigenvector, then a|ψ> is also an eigenvector.  The c_j can therefore only be uniquely defined up to a multiplicative constant.  That means that at most N - 1 of the above equations can be linearly independent.  (The determinant could not be zero otherwise.)  If N - 1 of the equations are linearly independent, then the solution for the c_j is unique up to an arbitrary multiplicative constant.  If less than N - 1 of the equations are linearly independent, then we can find more than one linearly independent solution for the c_j.  If this happens, the eigenvalue ω is said to be degenerate, and the associated eigenvectors form a subspace V_ω of V.

• The operator A is represented by the matrix
  
  
  in some basis.  
  It has eigenvalues -2 and 4.  
  Two independent solutions are associated with the eigenvalue -2, 
  c₁ = 0 , c₂ = 1 , c₃ = 0 , 
  and 
  c₁ = 1/√2 , c₂ = 0 , c₃ = -1/√2.

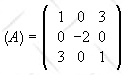
If the characteristic equation has N distinct roots, we can find N (up to a phase factor) unique, normalized, linearly independent eigenvectors which form a basis of V.  If the characteristic equation does not have N distinct roots, we may be able to find more than one linearly independent eigenvector associated with a multiple root and so still find N linearly independent eigenvalues.  But we may also find that only one eigenvector is associated with a multiple root and that the operator does not have a basis of eigenvectors.

Eigenvalues and eigenvectors of a Hermitian operator
The eigenvalues of a Hermitian operator are real.
Proof:
Let Ω|ω> = ω|ω >, then  <ω|Ω|ω > = ω<ω|ω >.
Take the adjoint.  <ω|Ω^†|ω> = ω^*<ω|ω >.
If Ω = Ω^†  then   <ω|Ω|ω > = ω^*<ω|ω>,  (ω - ω^*)<ω|ω > = 0.
Since |ω > ≠ 0, we have ω = ω^*.

Every Hermitian operator has at least one basis of orthonormal eigenvectors.  The matrix of the operator is diagonal in this basis and has its eigenvalues as its diagonal entries.
Proof:
The characteristic equation has at least one root, call it ω₁.  At least one non-zero eigenvector |ω₁> corresponds to this eigenvalue.  Let V_⊥1^n-1 be the subspace of all vectors orthogonal to |ω₁>.  As a basis for V we can now choose the normalized vector |ω₁> and n - 1 orthonormal vectors |V_⊥1¹>, |V_⊥1²>, |V_⊥1³>, ..., |V_⊥1^{n - 1}>.  In this basis the matrix of Ω has the following form:

.

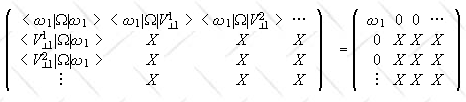We use the fact that Ω is Hermitian when we set <ω₁|Ω = ω₁<ω₁|.
The characteristic equation now takes the form
"(ω₁ - ω) times determinant of the square matrix denoted by X  =  0",
or (ω₁ - ω)∑_m=0^n-1c_mω^m = (ω₁ - ω)P^n-1(ω) = 0, where P^n-1(ω) is a polynomial of order n - 1.
The polynomial P^n-1 must also generate at least one root, call it ω₂, and a normalized eigenvector |ω₂>.  Define a subspace V_⊥1,2^{n - 2} of vectors in V_⊥1^{n - 1} orthogonal to |ω₂> and repeat the procedure.  Finally the matrix of Ω in the basis {|ω₁>, |ω₂>, ..., |ω_n>} becomes
.
Every |ω_i> is chosen from a subspace that is orthogonal to the previous one, therefore the basis {|ω_i>} is orthogonal.
Note: We did not assume that the eigenvalues are all distinct (non degenerate).

If the eigenvalues are degenerate, then there exist many bases of eigenvectors that diagonalize Ω.
Assume Ω|ω₁> = ω|ω₁> and Ω|ω₂> = ω|ω₂>. 
Then Ω(a₁|ω₁> + a₂|ω₂>) = ω(a₁|ω₁> + a₂|ω₂>) for any a₁, a₂ in F.  There exists a whole subspace spanned by |ω₁> and |ω₂>, whose elements are eigenvectors of Ω with eigenvalue ω.

Problem:

Consider a two dimensional vector space with an orthonormal basis {|1>, |2>}. 
Consider an operator whose matrix in that basis is  .

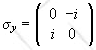(a)  Is the operator Hermitian?  Calculate its eigenvalues and eigenvectors.
(b)  Calculate the matrices which represent the projectors onto these eigenvectors.

• Solution:
  (a)  (σ_y)_ij =  (σ_y)_ji, therefore σ_y is Hermitian.  It is the matrix of a Hermitian operator.  Its eigenvalue are real.
  To find the eigenvalues β we set
  .
  
  β² - 1 = 0,  β = ±1.
  The eigenvector associated with  β₁ = 1 is |ψ₁> =  ∑_i=1²c_i|i>  with c₂ = i c₁. 
  |ψ₁> =  (1/√2)|1> + (i/√2)|2>.
  The eigenvector associated with  β₂ = -1 is |ψ₂> =  ∑_i=1²c_i|i>  with c₂ = -i c₁. 
  |ψ₂> =  (1/√2)|1> - (i/√2)|2>.
  (b) The projector onto |ψ_i> is P_i = |ψ_i><ψ_i|. 
  The matrix elements are (P_i)_jk = <j|ψ_i><ψ_i|k>.
  
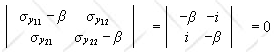  matrix of P₁: , matrix of P₂: .

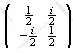The eigenvalues of a unitary operator are complex numbers of unit magnitude.  Eigenvectors with different eigenvalues are mutually orthogonal.
Proof:
Let U|u_i> = u_i|u_i>,  U|u_j> = u_j|u_j>.  
Let i, j denote eigenvectors with different eigenvalues if i ≠ j.  
Then <u_j|U^†U|u_i> = u_j^*u_i<u_j|u_i>.  
But U^†U = I, therefore <u_j|u_i> = u_j^*u_i<u_j|u_i>, or (1 - u_j^*u_i)<u_j|u_i> = 0.  
If i = j then <u_i|u_i> ≠ 0, therefore u_i^*u_i = 1. 
If i ≠ j then 1 - u_j^*u_i ≠ 0. 
(u_j ≠ u_i  -->  u_j^*u_i  ≠  u_i^*u_i  ≠  u_j^*u_j  ≠  1.)  
Therefore <u_j|u_i> = 0.

Assume both operators are degenerate.  By ordering the basis vectors we can get the matrix representation of A into the form
.

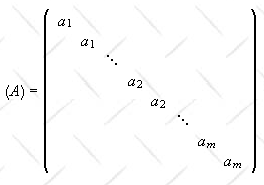This basis, however, is not unique.
The eigensubspace corresponding to every degenerate eigenvalue has an infinity of bases.

How does B appear in this basis?
AB|a_i^a> = BA|a_i^a> = a_iB|a_i^a>, where a = 1, ..., g_n and g_i denotes the degree of degeneracy of the eigenvalue a_i.  B|a_i^a> lies in the eigensubspace associated with the eigenvalue a_i.  Vectors from different eigensubspaces are orthogonal.  The matrix of B is therefore a block diagonal matrix.

.
The matrix of B in the eigensubspace is Hermitian and therefore can be diagonalized by trading the basis {|a_i>} for an eigenbasis of B_i.  The matrix of A remains diagonal, since we are choosing another orthonormal basis in a degenerate eigenspace.  If B is not degenerate in a given subspace, we will end up with a unique orthonormal basis of eigenvectors of both A and B.  If B is degenerate in any given subspace, the basis we find is not unique.  A third operator C, which commutes with A and B, ([A,C] = 0, [B,C] = 0) may still not be diagonal in this basis, and we may have to diagonalize the matrix of C in the eigensubspaces which belong to both A and B.  It is however always possible to find a set of operators {A, B, C, ...,} which commute by pairs and uniquely define a common eigenbasis.  Such a set of operators is called a complete set of commuting observables (C.S.C.O.).  It is generally understood that C.S.C.O. refers to the minimal set.