Suppose that an ion having s = 1, l = 0 is surrounded by an array of charges.  Its Hamiltonian is H = D[S_z² - 1/3 s(s + 1)I] + G(S_x² - S_y²) .  Assuming D/3 > G > 0.
(a)  Construct the energy matrix for this Hamiltonian.
(b)  Solve exactly for the energy eigenvalues.
(c)  Sketch the energy levels.
Given:   I is the identity matrix.

 
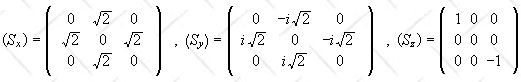
In this problem the units are chosen such that ħ = 1.

Solution

• (a)  You can solve this problem without knowing anything about the physical quantities represented by the operators S², L², S_x, S_y, and S_z.  L² and S² represent the operators for the square of the orbital angular momentum and the spin angular momentum of a spin 1 particle and S_x, S_y, and S_z represent the operators for the Cartesian components of the spin.  The eigenvalues of S² are s(s + 1)ħ² and the eigenvalues of L² are l(l + 1)ħ².  In this problem the units are chosen such that ħ = 1.
  S_z is diagonal.  The basis picked is an eigenbasis of S_z.  The eigenvalues of S_z are 1,0,-1.
  H = D[S_z² - 1/3 s(s + 1) I] + G(S_x² - S_y²).  D and G are numbers, S_x², S_y², and S_z² are matrices and s(s + 1) is a number.
  s = 1, s(s + 1) = 2, (1/3)s(s + 1) = 2/3.
  
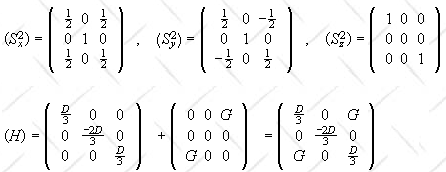
  (b)
  
  
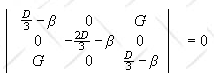
  -(D/3 - β)²(2D/3 + β) + G² (2D/3 + β) = 0.
  Either  (2D/3 + β) = 0, β₁ = -2D/3,  or  D/3 - β = ±G,  β₂ = D/3 + G,  β₃ = D/3 - G.
  The eigenvalues are β₁, β₂, and β₃.
  The eigenvector corresponding to the eigenvalue  β₁, β₂, and β₃ are
  .
  (c) We have found the eigenbasis of H.
  The eigenvalues are E₁ = -2D/3 < 0, E₂ = D/3 + G > 0,  E₃ = D/3 - G > 0.
  
  

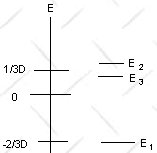
Problem:

The angular momentum operators {J_x, J_y, J_z} are central to quantum theory.  States are classified according to the eigenvalues of these operators when J is conserved by the respective Hamiltonian H.
(a)  What condition(s) is (are) necessary for all eigenstates of H to be eigenstates of J? 
An eigenstate of J is usually specified by |j,m_z>,
where J²|j,m_z>  =  j(j + 1)ħ²|j,m_z> and J_z|j,m_z> = m_zħ|j,m_z>.
(b)  We can substitute J_x or J_y for J_z in (a).  However a state cannot be simultaneously an eigenstate of J_z and J_x.  Derive the commutation relation for the angular momentum operators J_x and J_z, (i.e.  [J_x,J_z] = -iħJ_y) from the definition of the linear momentum operator.
(c)  Prove that it is indeed possible for a state to be simultaneously an eigenstate of J² = J_x² + J_y² +J_z² and J_z. 

Solution:

• Concepts::
  Commuting operators
• Reasoning:
  Two commuting observables can be measured simultaneously, i.e. the measurement of one does not cause loss of information obtained in the measurement of the other.  If we measure a complete set of commuting observables (C.S.C.O.), then the state of the system after the measurement is one element of an unique eigenbasis.  The results of the measurement specify the state completely.
• Details of the calculation:
  (a) It is possible to specify a common eigenbasis of two operators if they commute.  If one of the operators is non degenerate, then all of its eigenvectors are also eigenvectors of the other operator.  In order for all eigenstates of H to be eigenstates of J² and J_z we need [J²,H] = 0 and [J_z,H] = 0 and H is non degenerate.  (States with different j or m_z must have different energy eigenvalues E.)
  b) Assume the classical relationship J = r × p.
  J_x = yp_z - zp_y,  J_y = zp_x - xp_z,  J_z = xp_y - yp_x.
  For the quantum mechanical operators we then have
  J_x = YP_z - ZP_y,  J_y = ZP_x - XP_z,  J_z = XP_y - YP_x.
  [J_x,J_z] = [YP_z - ZP_y,XP_y - YP_x] = [YP_z,XP_y] + [ZP_y,YP_x] - [YP_z,YP_x] - [ZP_y,XP_y]
                                                                                        0               0
  = [YP_z,X]P_y + X[YP_z,P_y] + [ZP_y,Y]P_x + Y[ZP_y,P_x]
          0                                                  0
  = Z[P_y,Y]P_x +  X[Y,P_y]P_z = -iħ(ZP_x - XP_z) = -iħJ_y.
  
  (In general [J_i,J_j] = iħε_ijkJ_k.)
  (c) J² = J_x² + J_y² + J_z².  If [J²,J_z] = 0 then it is possible to find simultaneous eigenstates.
  [J²,J_z] = [J_x²,J_z] +  [J_y²,J_z] + [J_z²,J_z] = J_x[J_x,J_z] + [J_x,J_z]J_x + J_y[J_y,J_z] + [J_y,J_z]J_y
  = -iħ(J_xJ_y + J_yJ_x) + iħ(J_xJ_y + J_yJ_x) =0.

Problem:

The matrix  σ_x is defined by
.
Prove the relation exp(iασ_x) = I cosα + i σ_x sinα, where I is the 2 x 2 identity matrix.

• Solution:
  Functions of operators
  Let σ_x be the matrix of the Hermitian operator S_x in the {|1>,|2>} basis, <i|S_x|j> = (σ_x)_ij.
  exp(iαS_x) = cos(αS_x) + i sin(αS_x) = ∑_n=evenf_nαⁿ S_xⁿ + i ∑_n=oddf_nαⁿ S_xⁿ.
  <i|S_x²|j> = ∑_k=1²<i|S_x|k><k|S_x|j> = ∑_k=1²(σ_x)_ik(σ_x)_kj = δ_ij.
  Therefore S_x² = I,  S_xⁿ (n=even) = I,  S_xⁿ (n = odd) = IS_x = S_x.
  exp(iαS_x) =  ∑_n=evenf_nαⁿ I + i ∑_n=oddf_nαⁿ S_x = I cosα + i S_x sinα,
  exp(iασ_x) = I cosα + i σ_x sinα.
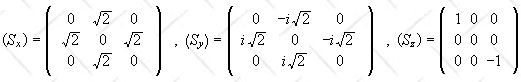
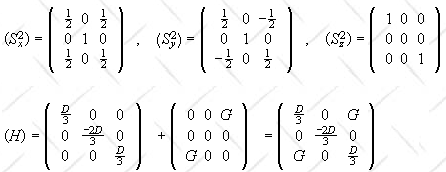
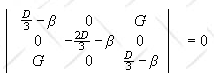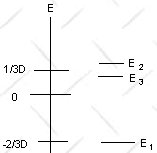