

Choosing a representation means choosing
an orthonormal basis in the state space E. Assume the set {|ui>} is a
discretely labeled basis and the set {|ωa>}
is a continuously labeled basis for E.
<ui|ui> = δij , <ωa|ωa'>
= δ(a - a’).
Any ket |ψ> may be written as |ψ> = ∑ici|ui>,
where ci = <ui|ψ>.
|ψ> = ∑i<ui|ψ>|ui> = ∑i|ui><ui|ψ>
= I|ψ> = |ψ>.
∑i|ui><ui is the projector into the subspace
spanned by {|ui>}. If {|ui>} is a basis then ∑i|ui><ui|
= I is the identity operator.
This is called
the closure relation.
Similarly, any ket |ψ> may be written as
|ψ> = ∫da c(a)|ωa>, where c(a) = <ωa|ψ>.
|ψ> = ∫da <ωa|ψ>|ωa> = ∫da |ωa><ωa|ψ>
= I|ψ> = |ψ>.
∫da |ωa><ωa| is the
projector into the subspace spanned by {|ωa>}.
If {|ωa>} is a basis then ∫da |ωa><ωa| = I is the identity operator.
This is called
the closure relation for a continuously
labeled basis.
In the basis {|ui>} the ket |ψ>
is completely specified by its components ci = <ui|ψ>.
The corresponding bra is completely specified by its
components ci* = <ψ|ui> in the
basis {<ui|}.
By convention, we represent a ket as a one column matrix of its components in a given
basis.
Representation of |ψ>: 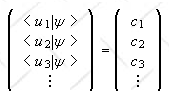
We represent a bra as one row matrix of its components in a given basis.
Representation of <ψ|: (<ψ|u1> <ψ|u2>
<ψ|u3> ... ) = (c1* c2* c3*
... )
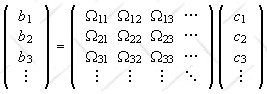
The column matrices are representations of the kets
|Φ>
and |ψ> and the square matrix is a representation of
the operator Ω in the {|ui>} basis.
The Ωij = <ui|Ω|
uj> are the matrix elements
of the operator Ω. The matrix elements are scalars.
By knowing the components of |ψ> in the basis {|ui>} and the actions
of the operator Ω on the basis vectors, we can calculate the components of |Φ> =
Ω|ψ> in the same basis.
The matrix elements of Ω are Ωij = <ui|Ω|uj>.
The matrix elements of Ω† are Ω†ij = <ui|Ω†|uj>
= <uj|Ω|ui>* = Ωji*.
If Ω is Hermitian, Ω = Ω†, then
Ωij = Ωji*.
In particular, Ωii = Ωii*.
The diagonal matrix elements of a
matrix representing a Hermitian operator are real.

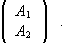
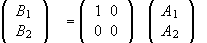 .
.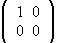 is the matrix of Ω in the {|xi>}
basis.
is the matrix of Ω in the {|xi>}
basis.