(a) Radioactive decay can produce neutrinos of either of two varieties, called ν_e and ν_μ.
There is considerable interest in the possibility that neutrinos have a small mass m₁, m₂.
Suppose that |ν_e> and |ν_μ>are linear combinations of the ortho-normal mass (or energy)
eigenstates |ν₁> and |ν₁>.
|ν_μ> = cosθ|ν₁> + sinθ|ν₂>,  |ν_e> = -sinθ|ν₁> + cosθ|ν₂>.
A nuclear reactor emits neutrinos of type ν_e.
A distance L away a detector is able to record the passage of ν_e. 
Assume that m_1,2c² << E_1,2, so that E = Pc + m²c³/2P.  Show that the intensity of ν_e at L relative to that at the source is
I(L) = 1 - sin²(2θ) sin²(c³∆m²L/(4ħE)) = 1 - sin²(2θ) sin²(1.27 L(m) ∆m²c⁴ (eV²)/E(MeV)).
Here  ∆m² = (m₁² - m₂²).

(b) Suppose that ∆m²c⁴ = 1 eV² and that a high energy accelerator is emitting neutrinos of energy 1 GeV. 
What is the optimum distance to place the detector to observe the effect of oscillations?

(c) The accelerator energy is reduced such that neutrinos emerge with only 1/45 of the energy that they had previously.
How does the optimal distance change?

Solution:
(a)  Equating mass and energy we assume that the mass eigenstates are the eigenstates of the Hamiltonian, which we assume does not explicitly depend on time.
H|ν₁> = E₁|ν₁>,  H|ν₂> = E₂|ν₂>.
U(t,t₀) = exp(-iH(t - t₀)/ħ) is the evolution operator. 
Therefore |ν₁(t)> = exp(-iE₁t/ħ)|ν₁(0)>,  |ν₂(t)> = exp(-iE₂t/ħ)|ν₂(0)>.
A second operator, which we denote by A, has eigenstates |ν_e>  and |ν_μ>.  It is the operator which distinguishes between the two varieties of neutrinos.
What is the probability that at time t a measurement of the observable A yields a neutrino of type ν_e? 
P_e(t) = |<ν_e|Ψ(t)>|², with |Ψ(0)> = |ν_e> = -sinθ|ν₁> + cosθ|ν₂>.
|Ψ(t)> = -sinθ exp(-iE₁t/ħ)|ν₁> + cosθ exp(-iE₂t/ħ)|ν₂>.
<ν_e|Ψ(t)> = (-sinθ<ν₁| + cosθ<ν₂|)(-sinθ exp(-iE₁t/ħ)|ν₁> + cosθ exp(-iE₂t/ħ)|ν₂>)
= sin²θ exp(-iE₁t/ħ) + cos²θ exp(-iE₂t/ħ).
|<ν_e|Ψ(t)>|² = sin⁴θ + cos⁴θ + 2 sin²θ cos²θ cos((E₁ - E₂)t/ħ)
= (3 + 4cos2θ + cos4θ)/8 + (3 - 4cos2θ + cos4θ)/8
+ ½(1 + cos2θ)(1 - cos2θ)cos((E₁ - E₂)t/ħ)
= 6/8 + (2/8)cos4θ + ½(1 - cos²2θ) cos((E₁ - E₂)t/ħ)
= 6/8 + (2/8)(1 - 2sin²2θ) + ½sin²2θ cos((E₁ - E₂)t/ħ)
= 1 - ½sin²2θ + ½sin²2θ cos((E₁ - E₂)t/ħ)
= 1 - sin²2θ[½ + ½cos((E₁ - E₂)t/ħ)]
= 1 - sin²2θ)sin²(E₁ - E₂)t/(2ħ)).
We have 
E = Pc + m²c³/2P.    [E = (p²c² + m²c⁴)^1/2 ≈ pc(1 + m²c²/2p²)]
E₁ - E₂ = (m₁² - m₂²)c³/(2P) =  ∆m²c³/(2P).
For t we have t = L/v ≈ L/c.
Therefore
(E₁ - E₂)t/(2ħ) = ∆m²c³L/(4ħPc) ≈ ∆m²c³L/(4ħE) since E ≈ Pc.
(E₁ - E₂)t/(2ħ) = ∆m²c⁴(eV²) (10^-6 MeV/eV) L(m)/(4E(MeV)(6.6*10^-16 eV s)(3*10⁸ m/s)
= 1.27 L(m) ∆m²c⁴ (eV²)/E(MeV).

(b)  sin²(1.27 L ∆m²c⁴/E) varies between 0 and 1.  To see oscillations there is no optimum distance.  One must map out the number of ν_e as a function of distance over several periods.
The first minimum in the number of ν_e occurs when  sin²(1.27 L ∆m²c⁴/E)  = 1 for the first time, i.e. when 1.27 L ∆m²c⁴/E = π/2 or when L = πE/(2*1.27 ∆m²c⁴) = 1.24 km.

(c)  L = 1.24 km/ 45 = 27 m.

Problem:

For the infinite well shown, the wave function for a particle of mass m, at t = 0, is
ψ(x, t = 0) = (2/a)^1/2sin(3πx/a).
(a)  Is ψ(x, t = 0) an eigenfunction of the Hamiltonian?
(b)  Calculate <X>, <P_x>, and <H> at t = 0. 

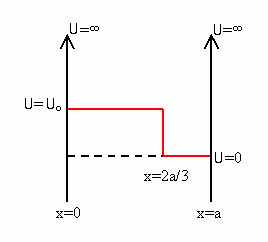
Solution:

• Concepts:
  The eigenfunctions of the infinite square well, the postulates of quantum mechanics.
• Reasoning:
  We recognize that the given wave function is an eigenfunction of the infinite square well.  The mean value of any observable A is <ψ|A|ψ>.
• Details of the calculation:
  (a)  ψ(x, t = 0) = (2/a)^1/2sin(3πx/a) is not an eigenfunction of the Hamiltonian.
  (b)  <x> = (2/a)∫₀^adx  x sin²(3πx/a)  = a/2.
   <p_x> = (2/a)∫₀^adx sin(3πx/a) (ħ/i) ∂sin(3πx/a)/∂x = C ∫₀^adx sin(3πx/a) cos(3πx/a) = 0.
  <H> = <T> + <U>. 
  ψ is an eigenfunction of the infinite square well with U = 0 for 0 < x < a.
  For the infinite square well we have <H> = E = <T>.
  Therefore  <T> = n²π²ħ²/(2ma²) =  9π²ħ²/(2ma²).
  <U> = ∫₀^a ψUψ dx = ∫₀^2a/3 ψU₀ψ dx = (2/a)∫₀^2a/3dx U₀ sin²(3πx/a) = 2U₀/3.
  <H> =  9π²ħ²/(2ma²) + 2U₀/3.

Problem:

A particle of mass m is inside a one-dimensional infinite well with walls a distance L apart.  One of the walls is suddenly moved by a distance L so that the wall separation becomes 2L.  The wall moves so suddenly that the particle wave function has no time to change during the motion.  Suppose that the particle is originally in the ground state ψ⁰.
(a)  What is its energy E₀ and wave function ψ⁰ before the width is doubled?
(b)  What are the energy eigenvalues after the width is doubled?
(c)  If we measure the energy after the width is doubled, what is the probability that it will not have changed?
(d)  If we measure the energy after the width is doubled, what is the probability that the particle will have lost some energy?
(e)  What is the expectation value of the energy before and after the doubling of the width?

Solution:

• Concepts:
  A particle in an infinite square well, the sudden approximation
• Reasoning:
  The sudden approximation can be used to calculate transition probabilities when the Hamiltonian changes rapidly.  The reaction time is so short that the transition amplitude <β|U(t₂,t₁)|α> is simply given by the overlap <β|α>.  The transition probability is |<β|α>|².  Here |α> is the eigenstate of the Hamiltonian before the transition and |β> is the eigenstate of the Hamiltonian after the transition.
• Details of the calculation:
  For a particle in an infinite well we have 
  ψ_n(x) = (2/L)^1/2sin(nπx/L), E_n = n²π²ħ²/(2mL²).
  (a)  ψ⁰(x) = ψ₁(x) = (2/L)^1/2sin(πx/L), E₀ = π²ħ²/(2mL²).  Note: the superscript 0 here stands for the ground state, not for the quantum number n.
  (b)  E_n' = n²π²ħ²/(2mL'²) = n²π²ħ²/(8mL²).
  (c)  For the energy to not have changed the particle must be found in the first excited state of the new potential (n = 2).
  P = |<ψ_f,2|ψ_i,1>|² = |(1/L)^1/2(2/L)^1/2∫₀^Ldx sin(2πx/(2L))sin(πx/L)|² = 1/2.
  (We integrate only from 0 to L since ψ_i(n=1) = 0 for x > L.)
  (d)  If we find the particle in the state n = 1 of the new potential then the particle has lost energy. 
  (If we do not find it in n = 1 then it has not lost energy.)
  P = |<ψ_f,1|ψ_i,1>|² = |(1/L)^1/2(2/L)^1/2∫₀^Ldx sin(πx/(2L))sin(πx/L)|²
  = (2/L²)[(2L/π)]∫₀^π/2dx' sin(x')sin(2x')|² = (8/π²)[(sin(x)/2 - sin(3x)/6))|₀^π/2]²
  = (8/π²)(4/6)² = 0.36.
  (e)  <E> = <H> = ∫₀^Ldx ψ_i,1(x) (p²/(2m)) ψ_i,1(x) = E₀ before and after the doubling of the width.

Assume the operator A commutes with the Hamiltonian H of a conservative physical system. 
Prove that in any state |ψ(t)> the probability of observing the eigenvalue a₀ is independent of time.

Solution:
If A commutes with H we can find a common eigenbasis of A and H.  Let {|E_nⁱ,a_m^j> } denote a common orthonormal eigenbasis of A and H for the state space E.
H |E_nⁱ,a_m^j> = E_n |E_nⁱ,a_m^j>,  A |E_nⁱ,a_m^j> = a_m |E_nⁱ,a_m^j>.
Here i and j the degeneracy of the eigenvalues.
|ψ(0)> may be expanded in terms of the basis vectors.
|ψ(0)> = ∑_ni,mj C_ni,mj |E_nⁱ,a_m^j>
Then
|ψ(t)> = ∑_ni,mj C_ni,mj |E_nⁱ,a_m^j> exp(-iE_nt/ħ).
The probability of observing the eigenvalue a₀ at time t is given by
P_a0(t) = ∑_n'i',j' <E_n'^i',a₀^j'|ψ(t)>|²
The sum is over all the quantum numbers associated with eigenvectors that have eigenvalue a₀.
<E_n'^i',a₀^j'|ψ(t)> = ∑_ni,mj C_ni,mj <E_n'^i',a₀^j'|E_nⁱ,a_m^j> exp(-iE_nt/ħ
= C_n'i',0j'  exp(-iE_n't/ħ
|<E_n'^i',a₀^j'|ψ(t)>|² = |C_n'i',0j'|²
P_a0(t) = ∑_n'i',j'|C_n'i',0j'|²,
which is independent of time.

Consider a one-dimensional problem.  Let the translation operator T(a) describe the operation T(a)ψ(x) =  ψ(x + a), where a is a constant displacement.
(a) Show that this operator commutes with the Hamiltonian, H = -(ħ²/(2m))∂²/∂x² + U(x), if the potential has the periodic property U(x) = U(x + a).
(b) Let ψ(x) be an eigenstate of T(a) with eigenvalue c.  Show that c is a constant of motion.

Solution:
(a)  ψ(x + a) = ∑_n(aⁿ/n!)dⁿψ(x)/dxⁿ = T(a)ψ(x)     (Taylor series expansion).
T(a) = ∑_n(aⁿ/n!)dⁿ/dxⁿ = exp(a d/dx) = exp((ia/ħ) (ħ/i)d/dx) = exp(iap/ħ),
since p = (ħ/i)d/dx.
H = (p²/(2m)) + U(x).
[T(a),H] = (2m)^-1[T(a),p²] + [T(a),U(x)].
[T(a),p²] = [exp(iap/ħ),p²] = ∑_n(1/n!)(ia/ħ)ⁿ[pⁿ,p²] = 0.
For any ψ(x) we have
[T(a),U(x)]ψ(x) = T(a)(U(x)ψ(x)) - U(x)(T(a)ψ(x))
= U(x + a)ψ(x + a) - U(x)ψ(x + a) = 0,
since U(x + a) = U(x). 
Thus [T(a),H] = 0.

(b) T(a)ψ(x) = cψ(x).  Since T(a) does not explicitly depend on time we have
(d/dt)<T(a)> = (iħ)^-1<[T(a),H]> = 0
Since ψ(x) is an eigenstate of T(a) we have <T(a)> = c.
Therefore dc/dt = 0,  c is a constant of motion.

ψ(x) represents the projection of |ψ> onto the basis vector |x>.  
What does T(a) do to the basis vectors {|x>} ?
T(a)ψ(x) = ψ(x + a),  T(a)<x|ψ> = <x + a|ψ>,
exp(a d/dx) <x|ψ> = <x|exp(iap/ħ)|ψ>
<x|exp(iap/ħ) = <x + a|,  exp(-iap/ħ)|x> = |x + a>,  exp(iap/ħ)|x> = |x - a>,