The physical meaning of the matrix elements of the density operator
ρ_nn(t) =  ∑_kp_kρ_nn^k(t) =  ∑_kp_k|c_n^k(t)|².
|c_n^k(t)|² is the probability that for a system in the state |ψ_k> a measurement of the observable whose eigenbasis is {|u_n>} will leave the system in the state |u_n>. 
ρ_nn(t) therefore represents the average probability of finding the system in the state |u_n>.
ρ_nn(t) is called the population of the state |u_n>.

ρ_np(t) = ∑_kp_kc_n^k(t)c_p^k*(t) (n ≠ p) expresses interference effects between the states |u_n> and |u_p> which appear when |ψ_k> is a linear superposition of states.  ρ_np(t) is the average of these interference effects.  It can be zero even if c_n^k(t)c_p^k*(t) is not zero.  In a statistical mixture of states the averaging can cancel out interference effects.  The off-diagonal matrix elements of ρ(t) are called coherences.  The populations and coherences obviously depend on the chosen basis.

Problem:

Consider a simple two-state quantum system with energy eigenvalues ħω_a and ħω_b and corresponding eigenkets |a> and |b> which are taken as the basis elements.
(a)  Write down the equation giving the time evolution of the eigenket |a> in the Schroedinger picture and in the Heisenberg picture.
(b)  Consider a pure state, which at time t = 0 is |Φ> = 2^-1/2(|a> + i|b>).  Write down the expression for |Φ(t)> in the Schroedinger and in the Heisenberg picture.
(c)  Consider a mixed state, which at t = 0 is defined by:
the system is in the state |ψ₁> = 2^-1/2(|a> + |b>) with 25% probability,
the system is in the state |ψ₂> = 2^-1/2(|a> - |b>) with 25% probability,
the system is in the state |ψ₃> = 2^-1/2(|a> + i|b>) with 50% probability.
Find the density matrix ρ in the {|a>,|b>} basis at t = 0.
(d)  Explain how the density operator evolves in time in the Schroedinger picture and in the Heisenberg picture.  Find the density matrix at time t for the mixed state in part (c) in each picture.
(e)  Consider the operator X which has the property X|a> = |b> and X|b> = |a>.  Find the expectation value of X at time t when the system is in the mixed state of part (c).  You may use either the Schroedinger or the Heisenberg picture for your calculations, but specify which picture you are using.

Solution:

Let |a_S> denote the state vector in the Schroedinger picture and let |a_H> denote the state vector in the Heisenberg picture.
(a)  iħ∂|a_s>/∂t = H|a_s>,  |a_s(t)> = U(t,0)|a_s(0)> = exp(-iHt/ħ)a_s(0)>.
|a_H> does not depend on time.

(b)  |Φ> = 2^-1/2(|a> + i|b>).
|Φ_s(t)> = 2^-1/2exp(-iHt/ħ)(|a> + i|b>) = 2^-1/2(exp(-iω_at)|a> + i exp(-iω_bt)|b>).
|Φ_H(t)> = 2^-1/2(|a> + i|b>).

(c)  The pure state density operator is ρ^k(t) = |ψ_k(t)><ψ_k(t)|.  The density operator for a statistical mixture of states is ρ(t) =  ∑_kp_kρ^k(t),  ∑_kp_k = 1.
Here p_k is the probability of being in state |ψ_k>.
ρ = ¼|ψ₁><ψ₁| + ¼|ψ₂><ψ₂| + ½|ψ₃><ψ₃|.

The density matrix elements in the eigenbasis of H are
 ρ₁₁ = <a|ρ|a>,  ρ₁₂ = <a|ρ|b>,  ρ₂₁ = <b|ρ|a>,  ρ₂₂ = <b|ρ|b>. 
<a|ψ₁> = √½,  <a|ψ₂> = √½,  <a|ψ₃> = √½,
<b|ψ₁> = √½,  <b|ψ₂> = -√½,  <b|ψ₃> = i√½,
Therefore ρ₁₁ = ½,   ρ₁₂ = -i/4,  ρ₂₁ = i/4,  ρ₂₂ = ½. 

(d)  dρ_s/dt = ∂ρ_S/∂t,  in the Schroedinger picture operators are constant in time unless they contain time explicitly.
dρ_H/dt = (∂ρ_S/∂t)_H +  (iħ)^-1[ρ_H,H_H].
dρ^k_s/dt = [∂/dt|ψ_k(t)>_S]<ψ_k(t)|_S +  |ψ_k(t)>_S[∂/dt<ψ_k(t)|_S]
= (iħ)^-1[H_Sψ_k(t)>_S<ψ_k(t)|_S - |ψ_k(t)>_S<ψ_k(t)|_SH_S]
= (iħ)^-1[H_s, ρ^k_s] = -(iħ)^-1[ρ^k_s,H_s].
Therefore
dρ_H/dt = -(iħ)^-1[ρ^k_s,H_s]_H +  (iħ)^-1[ρ_H,H_H] = 0.
In the Schroedinger picture dρ_s(t)/dt = (iħ)^-1[H_s,ρ_s], and in the Heisenberg picture dρ_H(t)/dt = 0.
In the Heisenberg picture the density operator is constant.  Therefore the density matrix is constant.

(e)  The expectation value of any observable A is <A>(t) = Tr{ρA}. 
In the Heisenberg picture we have <X>(t) = <a|ρX(t)|a> + <b|ρX(t)|b>.
dX_H/dt = (∂X_S/∂t)_H +  (iħ)^-1[X_H,H_H].

.

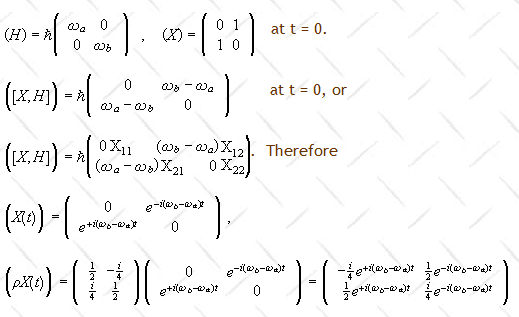<X> = -(i/4)[exp(+i(ω_a - ω_b)t) - exp(+i(ω_a - ω_b)t)]
= -(i/4)2i  sin((ω_a - ω_b)t) = ½ sin((ω_a - ω_b)t).