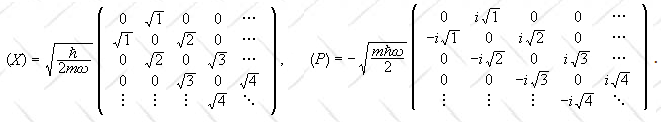Consider a particle of mass m moving in a potential energy function U(x) = ½kx². 
The force on the particle is given by F(x) = -dU(x)/dx = -kx.
The motion of the classical particle is governed by Newton’s second law md²x/dt² = -kx.
The general solution to this equation is x = x_Mcos(ωt + φ), with ω² = k/m.
We have dx/dt = -ωx_Msin(ωt + φ),  T = ½m(dx/dt)² = ½mω²x_M²sin²(ωt + φ),
E = T + U = ½mω²x_M²sin²(ωt + φ) + ½mω²x_M²cos²(ωt + φ) = ½mω²x_M².
The total energy is independent of time, we have a conservative system.

To make the transition to Quantum Mechanics we express E in terms of p and x and then replace the classical quantities p and x by their corresponding quantum mechanical operators P and X.
E = T + U = ½p²/m + ½mω²x² --> H = ½P²/m + ½mω²X².

Let us define some new operators and investigate their properties. Define
a = (2)^-1/2(X_s + iP_s), and its adjoint, a^† = (2)^-1/2(X_s - iP_s).
Then X_s = (2)^-1/2(a^† + a),  P_S = i(2)^-1/2(a^† - a).
Note that a and a^† do not commute.
[a,a^†] = ½[(X_s + iP_s), X_s - iP_s)] = ½[-i[X_s,P_s] + i[P_s,X_s] = ½(1 + 1) = 1.

Now we study the product operator a^†a.
a^†a = ½(X_s - iP_s)(X_s + iP_s) = ½(X_s² + P_s²  + iX_sP_s - iP_sX_s) =  ½(X_s² + P_s²  - 1).
Similarly, aa^† = ½(X_s² + P_s²  + 1).
We may therefore write H_s = a^†a + ½ = aa^† - ½ = ½(aa^† + a^†a).

Define the number operator N = a^†a. 
Then H_s = N + ½.  H_s and N have common eigenstates, finding the eigenstates of N is equivalent to finding the eigenstates of H_s and H. 
The operator N does not commute with a and a^†.
[N,a] = [a^†a,a] = a^†[a,a]  + [a^†,a]a = -a.
[N,a^†] = [a^†a,a^†] = a^†[a,a^†]  + [a^†,a^†]a = a^†.

We will now study some of the properties of the eigenstates of N and therefore the eigenstates of  H_s and H. 

(a)  The eigenvalues of N are positive.
Proof:  Let |Φ_ν> be an eigenstate of N with eigenvalue ν. 
N|Φ_ν> = ν|Φ_ν>.
Find the norm of the vector a|Φ_ν>.
|a|Φ_ν>|² = <Φ_ν|a^†a|Φ_ν> = <Φ_ν|N|Φ_ν> = ν<Φ_ν|Φ_ν> ≥ 0,
since the norm is always positive, and <Φ_ν|Φ_ν> ≥ 0  -->  ν ≥ 0.

(b)  If |Φ_ν> is an eigenstate of N with eigenvalue ν ≥ 1 and <Φ_ν|Φ_ν> ≠ 0 then a|Φ_ν> is an eigenstate of N with eigenvalue ν - 1. 
If |Φ_ν> is an eigenstate of N with eigenvalue ν < 1 then ν = 0 and a|Φ_ν> = a|Φ₀> = 0.
Proof:  |a|Φ_ν>|² =  ν > 0, unless ν = 0.
[N,a]|Φ_ν> = -a|Φ_ν>.  Na|Φ_ν> = aNΦ_ν> - a|Φ_ν> = (ν - 1)a|Φ_ν>.
a|Φ_ν> is an eigenstate of N with eigenvalue ν - 1. 
a|Φ_ν> is non zero unless ν = 0.  But the eigenvalues have to be positive.  Therefore if ν < 1 we need a|Φ_ν> = 0 which requires ν = 0.

(c)  If |Φ_ν> is an eigenstate of N with eigenvalue ν ≥ 0 and <Φ_ν|Φ_ν> ≠ 0 then a^†|Φ_ν> is an eigenstate of N with eigenvalue ν + 1.
Proof: | a^†|Φ_ν>|² = <Φ_ν|aa^†|Φ_ν> = <Φ_ν|a^†a + 1|Φ_ν> = (ν + 1)<Φ_ν|Φ_ν> > 0.
[N,a^†]|Φ_ν> = a^†|Φ_ν>,  Na^†|Φ_ν> = a^†N|Φ_ν> + a^†|Φ_ν>  = (ν + 1) a^†|Φ_ν>.

(d)  The eigenvalues of N are the non negative integers.
Proof:  N has at least one non-zero eigenvector with eigenvalue ν.  
(It is a Hermitian operator).  
N|Φ_ν> = ν|Φ_ν>.
Then |Φ_ν-1> = a|Φ_ν> is also an eigenvector if (ν - 1) > 0, 
|Φ_ν-n> = aⁿ|Φ_ν>is also an eigenvector if (ν - n) > 0.  
But for some n’ = n + 1 the number ν - n’ will become smaller than zero.  
Therefore |Φ_ν-n> must be zero.  
But a|Φ_ν-n> is only zero if |Φ_ν-n> = |Φ₀> or (ν - n) = 0.  
This means that n is a non-negative integer.
If |Φ_n> is a non-zero eigenvector of N with integer eigenvalue n, then the |Φ_n’> , n’ = 0, 1, 2, ... are also eigenvectors.  (We can generate these eigenvectors by applying a or a^† to |Φ_n> . )
The eigenvectors of N are {|Φ_n> } with eigenvalues {n}, where n is a non-negative integer.
The eigenvectors of H_s are {|Φ_n> } with eigenvalues {n + ½}.
The eigenvectors of H are {|Φ_n> } with eigenvalues {(n + ½)ħω}.
The energy of the harmonic oscillator is quantized.
The ground state energy is ½ħω. The energy levels are evenly spaced.

(e)  The ground state of N or H_s or H is not degenerate.
Proof:  N|Φ₀> = 0,  a|Φ₀> = 0,  (2)^-1/2(X_s + iP_s)|Φ₀> = 0, 
(2)^-1/2((mω/ħ)^1/2X + i(mωħ)^-1/2P)|Φ₀> = 0.
(mωX + iP)|Φ₀> = 0.  In the {|x>} representation this becomes
mω<x|X|Φ₀> + i<x|P|Φ₀> = 0,  mωx<x|Φ₀> + i((ħ/i)∂/∂x)<x|P|Φ₀> = 0,
(mωx/ħ)Φ₀(x) + ∂/∂x)Φ₀(x) = 0, 
Φ₀(x) = Cexp(-½mωx²/ħ)
is the solution to this first order differential equation.  It is unique up to a multiplicative constant C.  Therefore there exists only one normalized Φ₀(x) and |Φ₀> with the eigenvalue 0.  The eigenstate corresponding to the lowest eigenvalue of  N or H_s or H  is not degenerate.
By induction we can now proof that all eigenstates of  N or H_s or H are not degenerate.

The eigenvectors {|Φ_n> } of  N or H_s or H are a basis for the state space E_x of a particle in a one dimensional problem.  The |Φ_n> are orthogonal since all eigenvalues are not degenerate.  We now want to choose a normalized set {|Φ_n> }.

• Assume |Φ₀> is normalized, <Φ₀|Φ₀> = 1.  
  The normalized vector |Φ₁> is |Φ₁> = c₁a^†|Φ₀>. 
  If <Φ₁|Φ₁> = 1, then |c₁|²<Φ₀|aa^†|Φ₀> = |c₁|² <Φ₀|a^†a + 1|Φ₀> = |c₁|²  = 1. 
  Therefore |Φ₁> = a^†|Φ₀>.
• The normalized vector |Φ_n> is |Φ_n> = c_na^†|Φ_n-1>.
• If <Φ_n|Φ_n> = 1, then |c_n|²<Φ_n-1|aa^†|Φ_n-1> = |c_n|²<Φ_n-1|a^†a + 1|Φ_n-1> = n|c_n|²  = 1.  
  Therefore |Φ_n> = n^-1/2a^†|Φ_n-1>,
  |Φ_n> = n^-1/2(n-1)^-1/2(a^†)²|Φ_n-2> = n^-1/2(n-1)^-1/2 ... 2^-1/2(a^†)ⁿ|Φ₀>

  The set {|Φ_n> = (n!)^-1/2(a^†)ⁿ|Φ₀>} forms an orthonormal basis for E_x.
  <Φ_n|Φ_n'> = δ_n,n',  ∑_n|Φ_n><Φ_n| = I.
  Let {|Φ_n>} denote this orthonormal eigenbasis of the operator H = ½P²/m + ½mω²X².
  H|Φ_n> = (n + ½)ħω|Φ_n>.

• The results of operating with a or a^† on |Φ_n> are given by
  a|Φ_n> = √(n) |Φ_n-1>,  a^†|Φ_n> = √(n+1) |Φ_n+1>.

  The matrices representing a and a^† in the {|Φ_n>} basis therefore are
  
  
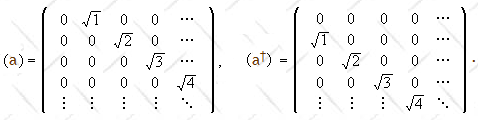
  The order of the basis vectors is (|Φ₀>, |Φ₁>, |Φ₂>, ...),
  <Φ_n|a|Φ_n'> = √(n') δ_n,n'-1,   <Φ_n|a^†}Φ_n''> = √(n'+1) δ_n,n'+1.  

• In terms of a and a^† the observables X an P are given by
  X = (ħ/(2mω))^1/2(a^† + a),  P = i(mħω/2)^1/2(a^† - a).
  The matrices representing X and P therefore are
  
  X and P are Hermitian operators.