There are two energy levels, E₊ = ħω₀/2 and E_- = -ħω₀/2, separated by ħω₀.
We define the Bohr frequency f_+- = |E₊ - E_-|/h = |ω₀|/(2π).
In general, the Bohr frequencies of a system whose energy eigenvalues are {E_n} are defined as
f_nn' = |E_n - E_n'|/(2πħ).
Note: If B ≈ B₀u then H = ω₀S_u.  For silver atoms γ is negative, ω₀ is positive , E₊ > E_- .

Assume a system in an arbitrary state
|ψ> = cos(θ/2)exp(-iφ/2)|+> + sin(θ/2)exp(iφ/2)|->
with  0 ≤ θ ≤ π  and  0 ≤ φ ≤ 2π  is placed into a uniform magnetic field B ≈ B₀k at t = 0.
The system evolves and we have
|ψ(t)> = U(t,0)|ψ(0)> = exp(-iHt/ħ)|ψ(0)> = exp(-iω₀S_zt/ħ)|ψ(0)>.
|ψ(t)> = cos(θ/2)exp(-i(φ + ω₀t)/2)|+> + sin(θ/2)exp(i(φ + ω₀t)/2)|->
= cos(θ/2)exp(-iφ'/2)|+> + sin(θ/2)exp(iφ'/2)|->,
where φ' = φ + ω₀t.
|ψ(t)> is an eigenvector of S_u’ , (u' is characterized by θ and φ'), while |ψ(0)> is an eigenvector of S_u , (u is characterized by θ and φ ).  The vector u' defining S_u' =  S∙u' revolves around the z-axis with angular frequency ω₀ ∝ B₀.  Its component along the z-axis remains constant, while its component perpendicular to the z-axis rotates with angular velocity ω₀.  This is the quantum mechanical analog of the rotation of the classical magnetic moment m and is called Larmor precession.

<S_z(t)> = <ψ(t)|S_z|ψ(t)> = (ħ/2)cos²(θ/2) - (ħ/2)sin²(θ/2)
= (ħ/2)½(1 + cosθ) - (ħ/2)½(1 - cosθ) = (ħ/2)cosθ.
S_z is a constant of motion.

<S_x(t)> = <ψ(t)|S_x|ψ(t)> = cos²(θ/2)<+|S_x|+> + sin²(θ/2)<-|S_x|->
+ cos(θ/2)sin(θ/2)exp(iφ')<+|S_x|-> + cos(θ/2)sin(θ/2)exp(-iφ')<-|S_x|+>.

.

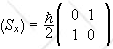<S_x(t)> = (ħ/2)cos(θ/2)sin(θ/2) 2cosφ' =  (ħ/2)sinθ cos(φ + ω₀t).

Similarly,  <S_y(t)> = (ħ/2)sinθ sin(φ + ω₀t).
S_x and S_y are not constants of motion.  Their expectation values oscillate with the single Bohr frequency |ω₀|/(2π).  The mean values of S_x, S_y, and S_z behave like the components of the classical angular momentum undergoing Larmor Precession.

Problem:

At t = 0 the x-component of the spin of a spin ½ particle is measured and found to be ħ/2.  At t = 0 the particle is therefore in the |+>_x eigenstate of the S_x operator.  The particle is confined to a region with a uniform magnetic field B = B₀k, its Hamiltonian is H = ω₀S_z.  The eigenstates of H are |+> and |->,
H|+> = (ħω₀/2)|+> and H|-> = -(ħω₀/2)|->.
|+>_x can be written as a linear combination of eigenstates of H.
(a)  Find the probability of measuring S_x = ħ/2 at t = T.
(b)  What is the mean value of S_x, <S_x>, at t = T?
(c)  Find the probability of measuring S_z = ħ/2 at t = T.

Solution:

• Concepts:
  The two dimensional state space of a spin ½ particle, the evolution operator, the postulates of Quantum Mechanics
• Reasoning:
  The state space corresponding to the observable S_z of a spin ½ particle is two-dimensional.  We denote the eigenvectors of S_z by |+> and |->.  The Hamiltonian of the system is H = ω₀S_z.  The evolution operator is exp(-iHt/ħ).  We use the evolution operator to find the state of the system at time T and then answer the questions using the postulates of Quantum Mechanics.

• Details of the calculation:
  (a)  The matrix of S_x in the eigenbasis of S_z is
  .
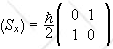  The eigenvectors of S_x are |+>_x and |->_x.
  |±>_x = (1/√2)(|+> ± |->).
  |ψ(t)> = U(t,0)|ψ(0)> = U(t,0)|+>_x = (1/√2)exp(-iHt/ħ)(|+> + |->).
  |ψ(t)> = (1/√2)(exp(-iω₀t/2)|+> + exp(-iω₀t/2)|->).
  P(S_x=ħ/2,T) = |_x<+||ψ(t)>|² = ¼|(<+| + <-|)(exp(-iω₀T/2)|+> + exp(-iω₀T/2)|->)|²
  = ¼|exp(-iω₀T/2)|+> + exp(-iω₀T/2)|² = cos²(ω₀T/2).

  (b) P(S_x=-ħ/2,T) = 1 - cos²(ω₀T/2) = sin²(ω₀T/2).
  <S_x(T)> = (ħ/2)[cos²(ω₀T/2) - sin²(ω₀T/2)] = (ħ/2)cos(ω₀T).

  (c) P(S_z=ħ/2,T) = |<+|ψ(t)>|² = ½|<+|(exp(-iω₀t/2)|+> + exp(-iω₀t/2)|->)|² = ½.
  The probability of measuring S_z = ħ/2 is independent of t.