Problem 1, solution

Problem 2, solution

The common eigenfunctions of S² and S_z are

|11>=|++>,
|10>=½^1/2(|+->+|-+>),
|1-1>=|-->,
|00>=½^1/2(|+->-|-+>).

From symmetry we therefore have that the common eigenfunctions of S² and S_x are

|11>_x=|++>_x,
|10>_x=½^1/2(|+->_x+|-+>_x),
|1-1>_x=|-->_x,
|00>_x=½^1/2(|+->_x+--+>_x).

We have

|++>_x=½^1/2(|+>+|->)Ľ^1/2(|+>+|->)=½(|++>+|+->+|-+>+|-->).
|-->_x=½^1/2(|+>-|->)Ľ^1/2(|+>-|->)=½(|++>-|+->-|-+>+|-->).
|+->_x=½^1/2(|+>+|->)Ľ^1/2(|+>-|->)=½(|++>-|+->+|-+>-|-->).
|-+>_x=½^1/2(|+>-|->)Ľ^1/2(|+>+|->)=½(|++>+|+->-|-+>-|-->).

Therefore

|11>_x=½(|++>+|+->+|-+>+|-->),
|10>_x=½^1/2(|++>-|-->),
|1-1>_x=½(|++>-|+->-|-+>+|-->),
|00>_x=½^1/2(|+->-|-+>).

Problem 3, solution  

(a)  The eigenvectors of S_y are |+>_y=2^-1/2(|+>+i|->) and |->_y=2^-1/2(|+>-i|->).

Therefore: |+>=2^-1/2(|+>_y+|->_y) and |->=(-i/2^1/2)(|+>_y-|->_y).

|y₁>=|+>_y.

|y₂>=(-i/6^1/2)(|+>_y+|->_y) -(i/3^1/2)(|+>_y-|->_y)=(-i)(0.986|+>_y+0.169|->_y

(b)  <y₁|y₂>=-i/6^1/2-i(2/6)^1/2=-i0.986 in the S_z basis.

      <y₁|y₂>=-i0.986 in the S_y basis.

(c)  |y₁(t)>=2^-1/2(exp(-iw₀t/2)|+>+iexp(iw₀t/2)|->) 

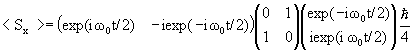
           =(h/4)i(-exp(-iw₀t)+exp(iw₀t))= -(h/2)sin(w₀t).

If <S_x>=±(h/2), then |y₁(t)> is an eigenvector of S_x.  This happens when w₀t=np/2, n=odd.

Problem 4, solution