Problem 1:
Two particles of mass m1 and m2 are separated by a
fixed distance r. Their center of mass is fixed at the origin of the coordinate system and they are free to rotate about their
center of mass. (The system is a "rigid rotator".)
(a) Write down the Hamiltonian of the system.
(b) Find the eigenvalues and eigenfunctions of this Hamiltonian. What is the
separation between adjacent levels? What is the degeneracy of the eigenvalues?
Solution:
- Concepts:
The time-independent Schroedinger equation in three dimensions, the
eigenfunctions of the orbital angular momentum operator.
- Reasoning:
We can write the Hamiltonian for the motion about the center of mass as that
of a fictitious particle of reduced mass m moving
in a central potential. We solve the Schroedinger equation in spherical
coordinates.
- Details of the calculation:
(a) The Hamiltonian of the rotator is L2/(2I)
where I is its moment of inertia,
I = m1r12 + m2r22
=
μr2,
μ = m1m2/(m1
+ m2).
(b) The eigenfunctions of H are the eigenfunctions of L2.
These are the spherical harmonics,
Ylm(θ,φ) = <r|l,m>.
The
eigenvalues are El =
l(l + 1)ħ2/(2I).
It is
customary to set B = ħ/(4πI), and
write El = Bhl(l + 1).
The separation between adjacent levels is El - El-1
= Bh[l(l + 1) - (l - 1)l] = 2Bhl.
The separation
increases linear with l. Each energy eigenvalue is 2l + 1 fold
degenerate.
Problem 2:
The wave function of a particle subjected to a spherically symmetric
potential U(r) is given by ψ(r) = (x + y + 3z)f(r).
(a) Is ψ an eigenfunction of L2? If so, what is its l
value? If not, what are the possible values of l we may obtain when L2
is measured?
(b) What are the probabilities for the particle to be found in various ml
states?
(c) Suppose it is known somehow that ψ(r) is an energy eigenfunction
with eigenvalue E. Indicate how we may find U(r).
Solution:
- Concepts:
The eigenfunctions of the orbital angular momentum operator, the spherical
harmonics
- Reasoning:
The common eigenfunctions of L2 and Lz are the
spherical harmonics. We have to write the given wave functions in terms of the
spherical harmonics.
- Details of the calculation:
ψ(r) = (x + y + 3z)f(r) = (rsinθcosφ
+ rsinθsinφ
- 3rcosθ)f(r)
= rf(r)(sinθcosφ
+ sinθsinφ
- 3cosθ)
= rf(r)(sinθ ½(eiφ + e-iφ) - i sinθ ½(eiφ -
e-iφ) - 3cosθ)
= rf(r)(sinθ ½eiφ (1 - i) + sinθ ½ e-iφ (1 + i) -
3cosθ)
= rf(r)(2-½exp(-iπ/2) sinθeiφ + 2-½exp(iπ/2)
sinθ e-iφ - 3cosθ).
Y1±1 =
∓(3/8π)1/2sinθ
exp(±iφ), Y10 = (3/4π)1/2cosθ.
ψ(r) = rf(r)(-exp(-iπ/2)(4π/3)1/2Y11(θ,φ)
+ exp(iπ/2)(4π/3)1/2Y1-1(θ,φ) - (12π)1/2Y10(θ,φ))
= rf(r)2√π(-exp(-iπ/2)(1/3)1/2Y11(θ,φ) + exp(iπ/2)(1/3)1/2Y1-1(θ,φ)
- (3π)1/2Y10(θ,φ))
= (44π/3)1/2rf(r)(-exp(-iπ/2)/111/2Y11(θ,φ)
+ exp(iπ/2)/111/2Y1-1(θ,φ) - 3/111/2Y10(θ,φ))
= R(r) (-exp(-iπ/2)/111/2Y11(θ,φ) + exp(iπ/2)/111/2Y1-1(θ,φ)
- 3/111/2Y10(θ,φ)).
The function of angle is normalized.
ψ(r) is an eigenfunction of L2 with eigenvalue
2ħ2, l = 1.
(b) The possible values of ml are 1, 0, -1.
P(ml = 1) = 1/11,
P(ml = -1) = 1/11,
P(ml = 0) = 9/11.
(c) The wave function ψklm(r,θ,φ)
= Rkl(r)Ylm(θ,φ) = [ukl(r)/r]Ylm(θ,φ)
is a product of a radial function Rkl(r) and the spherical harmonic Ylm(θ,φ).
The differential equation for ukl(r) is
[-(ħ2/(2m))(∂2/∂r2)
+ ħ2l(l+1)/(2mr2)
+ U(r)]ukl(r) = Eklukl(r).
Since ukl(r), Ekl and l are known, we can solve this
equation for U(r).
Problem
3, solution

Problem
4, solution
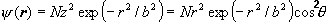 .
.
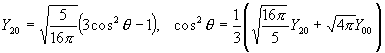 .
.
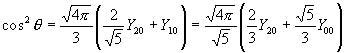 .
.
 .
.
(a) If L2 is measure we can obtain
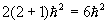 with probability 4/9 and 0 with
probability 5/9.
with probability 4/9 and 0 with
probability 5/9.
(b) If Lz is measured we obtain 0 with probability 1.
(c)
y(r) is not an eigenfunction of
L2.
y(r) is an eigenfunction of
Lz.


![]() .
.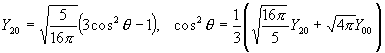 .
.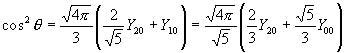 .
.![]() .
.![]() with probability 4/9 and 0 with
probability 5/9.
with probability 4/9 and 0 with
probability 5/9.