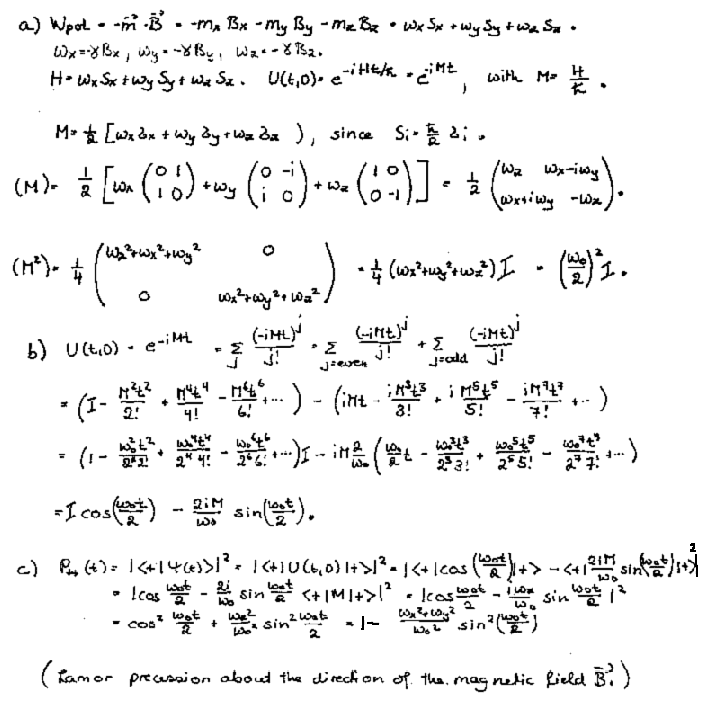Problem 1, solution
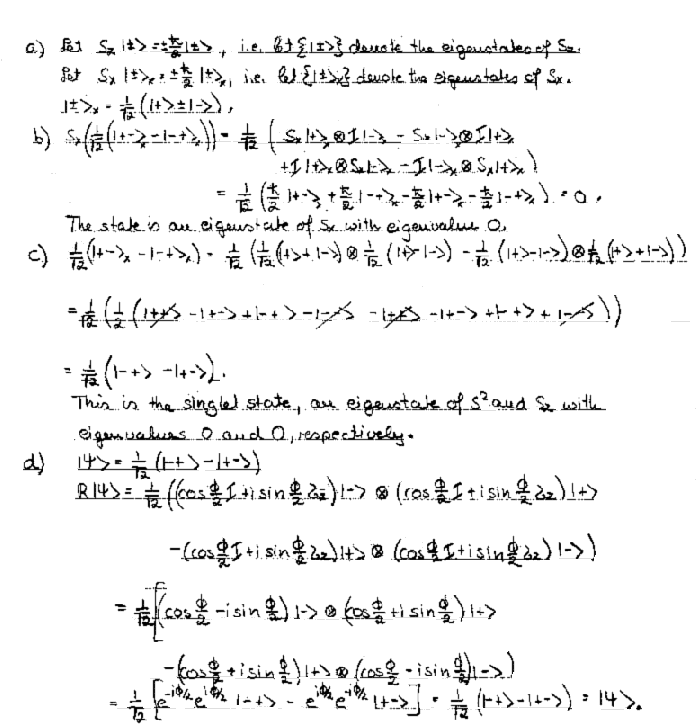
Problem 2, solution
(a) The z-component of B is constant, while the component of B perpendicular to the z-axis rotates ccw about the z-axis with frequency w.
(b) H(t)=-gS×B(t)=-gB0Sz-gB1(coswt Sx+sinwt Sy)=w0Sz+w1(coswt Sx+sinwt Sy)
Let U(R) be the rotation operator for a ccw rotation R(f) about the z-axis.
U(R)=exp(-(i/h)Szf)
|y(t)>=U(t,0)|y(0)>, U(R)|y(t)>=U(R)U(t,0)|y(0)>
U(R)
can be viewed as an operator that rotates every state vector ccw through an
angle f or an
operator that changes the basis vectors and therefore rotates the coordinate
system cw through an angle f.
Let f=-wt, then U(R) rotates the coordinate system ccw with angular frequency w. The coordinate system then rotates with the magnetic field.
Consider an infinitesimal rotation.
U(R)|y(dt)> = (I+(i/h)Szwdt)|y(dt)> = (I+(i/h)Szwdt)(I-(i/h)Hdt)|y(0)>
U(R)|y(dt)> = (I+(i/h)Szwdt)(I-(i/h)(w0Sz+w1(coswt Sx+sinwt Sy))dt)| +>
U(R)|y(dt)> = (I+(i/h)((w-w0)Sz-w1Sxcoswt-w1Sysinwt)dt)| +>
S is a vector observable, its components transform under rotation R as V’=R-1V.
For a ccw rotation R(f)
we have Vx’=Vxcosf+Vysinf.
Therefore Sx’=Sxcoswt+Sysinwt is the x-component of the observable S in a frame that rotates ccw with angular frequency w about the z-axis, i.e. in a frame that rotates with the magnetic field.
U(R)|y(dt)>=|y'(dt)>=(I+(i/h)((w-w0)Sz-w1Sx’)dt)|+>
|y'(dt)>=(I+(i/h)((w-w0)Sz’-w1Sx’)dt)|y’(0)>
|y'> denotes the state vector in a frame rotating ccw about the z-axis with angular frequency w.
In this frame the evolution operator is U(t,0)=exp(-(i/h)((w-w0)Sz’-w1Sx’)t).
The Hamiltonian therefore is H’=(w-w0)Sz’-w1Sx’.
The matrix of the Hamiltonian is
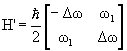
in the {|+>, |->} basis.
The eigenfunctions and eigenvalues are
E+=+(h/2)(Dw2+w12)1/2, |y'+>=cos(q/2)|+>+sin(q/2)|->,
E-=-(h/2)(Dw2+w12)1/2, |y'->=-sin(q/2)|+>+cos(q/2)|->,
where tanq=-w1/Dw, sinw=-w1/(Dw2+w12)1/2.
Therefore:
|y’(0)> = |+> = cos(q/2)|y'+>-sin(q/2)|y'->,
|y’(t)> = cos(q/2)exp(-(i/h)E+t)|y'+>-sin(q/2)exp((i/h)E+t)|y'->
= cos(E+t/h)[cos(q/2)|y'+>-sin(q/2)|y'->]-i sin(E+t/h)[cos(q/2)|y'+>+sin(q/2)|y'->]
= cos(E+t/h)|+>-i sin(E+t/h)[cos(q)|+>+sin(q)|->]=b+|+>+b-|->
To find the eigenfunctions in the lab frame we use U-1(R)|y’(t)> = |y(t)>.
exp(-(i/h)Szwt)|y’(t)> = exp(-iwt/2) b+|+>+exp(i/wt/2) b-|-> = |y(t)>.
We now have:
a+(t)= exp(-iwt/2)b+ = exp(-iwt/2)(cos(E+t/h)-i sin(E+t/h)cos(q))
a-(t)= exp(iwt/2)b- = -i exp(iwt/2)sin(E+t/h)sin(q)
Special case:
If
w=w0,
the Dw=0 and E+=(h/2)w1,
tanq=-w1/Dw=-
¥, q=-p/2, cos(q)=0,
sin(q)=-1.
Then
a+(t)= exp(-iwt/2) b+ = exp(-iwt/2)cos((w1/2)t),
a-(t)= exp(iwt/2) b- = i exp(iwt/2)sin((w1/2)t).
(c) P+-(t)=|a-(t)|2= sin2(E+t/h)sin2(q)=w12/(Dw2+w12) sin2((Dw2+w12)1/2t/2)
For the special case w=w0 P+-(t)= sin2((w1/2)t). Then P+-(t)= 1 if (w1/2)t=np/2, n=odd.
(d) |+> and |-> are both excited states and both decay with probability 1/t per unit time. If n atoms are excited at t=0, then at time t n exp(t/t) are still in an excited state. The atoms that are in an excited state flip between |+> and |->.
If an atom is excited at t=0, then the probability of
finding it in the state |-> at time t is exp(t/t) P+-(t). Assume
n atoms are excited per unit time. As t goes to infinity we find the total
number of atoms in the |-> state by summing up the contributions from all
prior time intervals, i.e. by calculating the integral
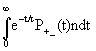 .
.
Use
 .
.
We multiply the number of atoms thus obtained by their probability of decay 1/t to find the number N which decay from the state |-> per unit time.
N=(n/2)w12/(Dw2+w12+(1/t)2)
N plotted versus Dw is a Lorentz curve with half width L=(w12+(1/t)2)1/2.
Dw=w-w0=w+gB0.
Problem
3, solution