Consider the one-dimensional potential step defined by U(x) = 0 , x < 0,  U(x) = U_0, x > 0.

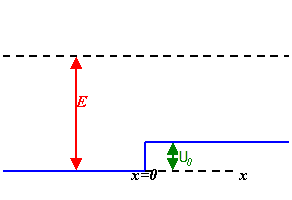
Suppose a wave incident from the left has energy E = 4U₀.  What is the probability that the wave will be reflected?

Solution:

• Concepts:
  This is a "square potential" problem.  We solve HΦ(x) = EΦ(x) in regions where U(x) is constant and apply boundary conditions.
• Reasoning:
  We are given a piecewise constant potential.  We have a potential that has a value of 0 for x < 0 and a value of U₀ (barrier) for  x > 0.  We are asked to find the the reflectance R.
• Details of the calculation:
  We have E > U₀.
  The most general solutions in regions 1, and 2 are
  Φ₁(x) = A₁exp(ik₁x) + A₁'exp(-ik₁x),
  Φ₂(x) = A₂exp(ik₂x),
  for particles incident from the left.
  Here k₁² = (2m/ħ²)E and k₂² = (2m/ħ²)(E - U₀).
  Φ is continuous at x = 0. Therefore A₁ + A₁' = A₂.
  (∂/∂x)Φ(x) is continuous at x = 0.  Therefore ik₁A₁ - ik₁A₁' = ik₂A₂ .
  We can then solve for A₁'/A₁.  We find A₁'/A₁ = (k₁ - k₂)/(k₁ + k₂).
  The reflectance R  = |A₁'/A₁|²  = 1 - 4k₁k₂/(k₁ + k₂)².
  k₁² = 8mU₀/ħ²,  k₂² = 6mU₀/ħ²,  k₁k₂ = (48)^1/2(mU₀/ħ²),
  R = 1 - 4(48)^1/2/(√8 + √6)² = 0.005

Problem 2:

You are given a one dimensional potential barrier of height U which extends from x = 0 to x = a.  A particle of mass m and energy E < U is incident from the left.
(a)  Derive expressions for the transmittance T and reflectance R for the barrier.
(b)  Show that T + R =  1.

Solution:

• Concepts:
  This is a "square potential" problem.  We solve HΦ(x) = EΦ(x) in regions where U(x) is constant and apply boundary conditions.
• Reasoning:
  We are given a piecewise constant potential.  We have a potential that has a value of U from x = 0 to x = a and is zero otherwise.  We are asked to find the transmittance T and reflectance R.
• Details of the calculation:
  Divide space into 3 regions;
  region 1: x < 0, region 2: 0 < x < a, region 3: x > a.
  (a)  potential barrier, E < U.
  The most general solutions in regions 1, 2, and 3 are
  Φ₁(x) = A₁exp(ikx) + A₁'exp(-ikx),
  Φ₂(x) = B₂exp(ρx) + B₂'exp(-ρx),
  Φ₃(x) = A₃exp(ikx).
  Here k² = (2m/ħ²)E and ρ² = (2m/ħ²)(U - E).
  The boundary conditions are that Φ(x) and (∂/∂x)Φ(x) are continuous at x = 0 and x = a.
  x = 0:  A₁ + A₁' = B₂ + B₂', ikA₁ - ikA₁' = ρB₂ - ρB₂'.
  x = a:  B₂exp(ρa) + B₂'exp(-ρa) = A₃exp(ika),
  ρB₂exp(ik₂a) - ρB₂'exp(-ρa) = ik_iA₃exp(ika).
  We need to solve these equations for A₃ and A₁' in terms of A₁.
  
  (i)  Solve for B₂ and B₂' in terms of A₃.
  B₂ = ½exp((ik - ρ)a)(1 + ik/ρ )A₃ = C A₃.
  B₂' = ½exp((ik + ρ)a)(1 - ik/ρ)A₃ = C' A₃.
  
  (ii)  Now solve for A₁ in terms of A₃ to find T.
  2A₁ = B₂ + B₂' + (ρ/ik)(B₂ - B₂') = (C + C' + (ρ/ik) (C - C'))A₃.
  A₁ = ([(k² - ρ²)/(2ikρ)]sinhρa + coshρa)exp(ika)A₃.
  T = |A₃/A₁|² = 4k²ρ²/[(k² - ρ²)²sinh²ρa + 4k²ρ²cosh²ρa]
  = 4k²ρ²/[(k² + ρ²)²sinh²ρa + 4k²ρ²].
  [cosh²x - sinh²x = 1.]
  T = 4E(U - E)/[U²sinh²[(2m(U - E)/ħ²)^1/2a] + 4E(U - E)].
  
  (iii)  Now solve for A₁^' in terms of A₁ to find R.
  A₁ + A₁' = B₂ + B₂' = (C + C')A₃.
  A₁ - A₁' = (ρ/(ik))(B₂ - B₂') = (ρ/(ik))(C - C')A₃.
  A₁(C + C' - (ρ/(ik))(C - C')) = A₁'(C + C' - (ρ/(ik))(C - C')).
  C + C' - (ρ/(ik))(C - C') = [[(k² - ρ²))/(ikρ)]sinhρa + coshρa]]exp(ika).
  C + C' - (ρ/(ik))(C - C') = [(k² + ρ²))/(ikρ)]sinhρa exp(ika).
  R = |A₁'/A₁|² = (k² + ρ²)²sinh²ρa/[(k² + ρ²)²sinh²ρa + 4k²ρ²],  or
  R = U²sinh²[(2m(U - E)/ħ²)^1/2a] /[U²sinh²[(2m(U - E)/ħ²)^1/2a] + 4E(U - E)].
  
  (b)  T + R = 4k²ρ²/[(k² + ρ²)²sinh²ρa + 4k²ρ²] + (k²+ ρ²)²sinh²ρa/[(k² + ρ²)²sinh²ρa + 4k²ρ²] = 1.

The one-dimensional square well shown in the figure rises to infinity at x = 0 and has range a and depth U₁.

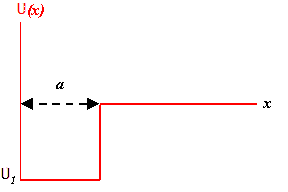
(a)  Derive the condition for a spinless particle of mass m to have two and only two bound states in the well.
(b)  Sketch the wave function of these two states inside and outside the well and give their analytic expressions.  These expressions may involve undetermined constants.

Solution:

• Concepts:
  Square potentials
• Reasoning:
  We want to solve for the bound states in a square well.
• Details of the calculation:
  (a)  Let region 1 extend from x = 0 to x = a and region 2 from x = a to infinity.
  For bound states we have E < 0. 
  Define k² = (2m/ħ²)(E + U₁), ρ² = (2m/ħ²)(-E), and k₀² = (2m/ħ²)U₁.
  Note: I am assuming that U₁ is a positive number denoting the depth, the potential energy at the bottom of the well is -U₁.
  In region 1 we have Φ₁(x) = A sin(kx), since  Φ₁(0) = 0.
  In region 2 we have Φ₂(x) = Bexp(-ρx), since Φ₂(∞) = 0.
  At x = a we need hat Φ(a) and (∂/∂x)Φ(x)|_a are continuous.
  A sin(ka) = B exp(-ρa)
  kA cos(ka) = -ρB exp(-ρa)
  Therefore cot(ka) = -ρ/k.
  1/sin²(ka) = 1 + cot²(ka) = (k² + ρ²)/k²  = k₀²/k².
  We can find a graphical solution by plotting |sin(ka)| and k/k₀ versus k.  The intersections of the two plots in regions where cot(ka) < 0 gives the values of k for which a solution exist.
  
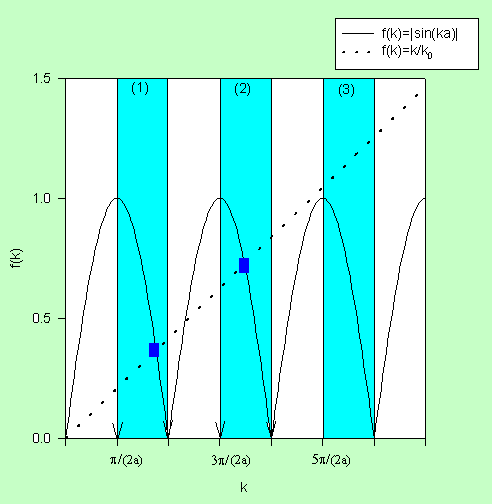
  It is possible to have no solutions, when π/(2k₀a) > 1.
  For only two solution to exist we need the following condition for the slope 1/k₀.
  2a/(5π) < 1/k₀ < 2a/(3π),  3π/(2a)  < k₀ < 5π/2a,  3π/(2a)  < ((2m/ħ²)U₁)^1/2 < 5π/2a.
  
  (b)  Inside the well Φ(x) = A sin(kx), outside the well for positive x > a, Φ(x) = Bexp(-ρx) = A sin(ka)exp(ρa)exp(-ρx), where k is a solution of |sin(ka)| = k/k₀, cot(ka) < 0, and ρ is determined once k is determined.
  

Consider the scattering of a particle of mass m and total energy  E = ħ²k²/(2m) under the influence of a localized one-dimensional potential.
(a)  Let the potential be a delta function potential well, U(x) = -aU₀δ(x) with a > 0 and U₀ = ħ²k₀²/(2m).  What are the asymptotic boundary conditions at x = ∞ and the matching conditions at x = 0 for the wave function?
(b)  Define the transmission coefficient T and the reflection coefficient R and find the relationship between T and R.
(c)  How does the transmission coefficient depend on E?
(d)  Now the potential is replaced by a double delta function potential well.  The delta functions are a distance b apart, i.e. U(x) = -aU₀δ(x) - aU₀δ(x - b).  By inspecting the matching conditions without solving the algebra equation, explain intuitively the limiting behavior of the transmission coefficient T for E --> 0 and E --> ∞.

Solution:

• Concepts:
  This is a "square potential" problem.  We solve HΦ(x) = EΦ(x) in regions where U(x) is constant and apply boundary conditions.
• Reasoning:
  U(x) = 0 everywhere except at x = 0 (and x = b in part d).
• Details of the calculation:
  (a) Φ is continuous at x = 0.  ∂Φ/∂x has a finite discontinuity at x = 0.
  Assume the particle is incident from the left.
  Φ₁(x) = A₁ exp(ikx) + A₁'exp(-ikx) for x < 0.  k² = 2mE/ħ².
  Φ₂(x) = A₂ exp(ikx)  for x > 0.
  (b)  Φ is continuous at x = 0.  Φ₁(0) = Φ₂(0).  A₁ + A₁’ = A₂.
  ∂Φ/∂x has a finite discontinuity at x = 0.
  ∂²Φ(x)/∂x² + (2m(E - U)/ħ²)Φ(x) = 0.
  Let us evaluate this equation at x = ε and at x = -ε and write down a difference equation.
  ∂Φ_ε(x₁ + ε)/∂x + ∂Φ_ε(x₁ - ε)/∂x = -(2m/ħ²)∫_x1-ε^x1+ε (E + aU₀δ(x)) Φ(x) dx
  = -(2maU₀/ħ²)Φ(0).
  iA₁k – iA₁’k = iA₂k + A₂2maU₀/ħ²,  A₁ – A₁’ = A₂ + A₂2maU₀/(ikħ²)  = [1 + 2maU₀/(ikħ²)]A₂.
  Eliminate A₁’: 
  2A₁ = [2 + 2maU₀/(ikħ²) ]A₂,  A₂/A₁ = 1/[1 + maU₀/(ikħ²)] = ikħ²/(ikħ² + maU₀).
  T(E) = (k|A₂|²)/(k|A₁|²) = ħ⁴k²/(ħ⁴k² + m²a²U₀²) = E/(E + ma²U₀²/(2ħ²)).
  Eliminate A₂:
  A₁ – A₁’ = A₂ - A₂2maU₀/(ikħ²)  = [1 - 2maU₀/(ikħ²)](A₁ + A₁’).
  A₁'/A₁ =  2maU₀/(ikħ²)/ [2 - 2maU₀/(ikħ²)] = -maU₀/(ikħ² - maU₀).
  R(E) = (k|A₁'|²)/(k|A₁|²) =  ma²U₀²/(ħ⁴k² + m²a²U₀²).
  T + R = 1
  (c)  T(E) = E/(E + ma²U₀²/(2ħ²)).
  As E --> 0, T --> 0,   R --> 1.
  As E --> ∞, T --> 1,   R --> 0.
  (d)  As E --> 0, nothing is transmitted past the first delta function.
  As E --> ∞,everything is transmitted across both delta functions.