Problem 1:

(a)  Calculate the transmission coefficient for a particle with mass m and kinetic energy E < U₀ passing through the rectangular potential barrier
U(x) = 0 for x < 0, U(x) = U₀ > 0 for 0 < x < a, and U(x) = 0 for x > a.
(b)  Show that for E << U₀ and  2mU₀a²/ħ² >> 1 the transmission coefficient can be written as  T ≈ (16E/U₀)exp[-2(2mU₀/ħ²)^1/2a].
(c)  Many heavy nuclei decay by emitting an alpha particle.  In a simple one-dimensional model, the potential barrier the alpha particles have to penetrate can be approximated by
U(r) = 0 for r < R₀,  U(r) = U₀R₀/r for r > R₀,
where R₀ is the radius of the nucleus and U₀ is the barrier height for r₀ = R.  The energy E of the alpha particle can be assumed to be much smaller than U₀.  For a non constant potential barrier the expression for the transmission coefficient found in part (b) can be used as a guide.  Assume that for E << U₀, we have T ≈ exp[-2∫_R1^R2 dr (2m(U(r) - E)/ħ²)^1/2].
The integration limits R₁ and R₂ are determined as solutions to the equation U(r) = E. 
Calculate the alpha transmission coefficient and the decay constant λ, i.e. the decay probability per second.

Solution:

• Concepts:
  This is a "square potential" problem.  We solve HΦ(x) = EΦ(x) in regions where U(x) is constant and apply boundary conditions.
• Reasoning:
  We are given a piecewise constant potential.  We are asked to find the transmittance T.
• Details of the calculation:
  (a)  Divide space into 3 regions;
  region 1: x < 0, region 2: 0 < x < a, region 3: x > a.
  (a)  potential barrier, E < U₀.
  The most general solutions in regions 1, 2, and 3 are
  Φ₁(x) = A₁exp(ikx) + A₁'exp(-ikx),
  Φ₂(x) = B₂exp(ρx) + B₂'exp(-ρx),
  Φ₃(x) = A₃exp(ikx).
  Here k² = (2m/ħ²)E and ρ² = (2m/ħ²)(U₀ - E).
  The boundary conditions are that Φ(x) and (∂/∂x)Φ(x) are continuous at x = 0 and x = a.
  x = 0:  A₁ + A₁' = B₂ + B₂', ikA₁ - ikA₁' = ρB₂ - ρB₂'.
  x = a:  B₂exp(ρa) + B₂'exp(-ρa) = A₃exp(ika),
  ρB₂exp(ik₂a) - ρB₂'exp(-ρa) = ik_iA₃exp(ika).
  We need to solve these equations for A₃ and A₁' in terms of A₁.
  
  (i)  Solve for B₂ and B₂' in terms of A₃.
  B₂ = ½exp((ik - ρ)a)(1 + ik/ρ )A₃ = C A₃.
  B₂' = ½exp((ik + ρ)a)(1 - ik/ρ)A₃ = C' A₃.
  
  (ii)  Now solve for A₁ in terms of A₃ to find T.
  2A₁ = B₂ + B₂' + (ρ/ik)(B₂ - B₂') = (C + C' + (ρ/ik) (C - C'))A₃.
  A₁ = ([(k² - ρ²)/(2ikρ)]sinhρa + coshρa)exp(ika)A₃.
  T = |A₃/A₁|² = 4k²ρ²/[(k² - ρ²)²sinh²ρa + 4k²ρ²cosh²ρa]
  = 4k²ρ²/[(k² + ρ²)²sinh²ρa + 4k²ρ²].
  [cosh²x - sinh²x = 1.]
  T = 4E(U₀ - E)/[U₀²sinh²[(2m(U₀ - E)/ħ²)^1/2a] + 4E(U₀ - E)].

  (b)   E << U₀ and  2mU₀a²/ħ² >> 1.
  sinh(x) = ½(e^x - e^-x) ≈ ½e^x, if x >> 1.
  Therefore
  T ≈ 4E(U₀ - E)/[¼U₀²exp[2(2m(U₀ - E)/ħ²)^1/2a] + 4E(U₀ - E)]
  ≈ 4EU₀/[¼U₀²exp[2(2mU₀/ħ²)^1/2a] + 4EU₀)]
  ≈ (16E/U₀)exp[-2(2mU₀/ħ²)^1/2a].

  (c)  Assume that T ≈ exp[-2∫_R1^R2 dr (2m(U(r) - E)/ħ²)^1/2].
  

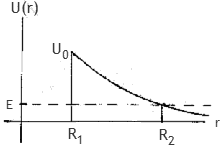
  R₁ = R₀,  R₂ = U₀R₀/E,  R₂ >> R₁.
  ∫_R1^R2 dr (U(r) - E)^1/2 = ∫_R1^R2 dr (U₀R₀/r - U₀R₀/R₂)^1/2
  = (U₀R₀)^1/2∫_R1^R2 dr (1/r - 1/R₂)^1/2.
  ∫_R1^R2 dr (1/r - 1/R₂)^1/2 = ∫_R1^R2 dr [(R₂ - r)/(rR₂)^]1/2
  = √R₂[(R₁/R₂ - (R₁/R₂)²)^1/2 + π/2  - tan^-1(R₁/(R₂ - R₁))^1/2 
  -->  √R₂ π/2  if R₂ >> R₁.
  T ≈ exp[-√(2m/E) πU₀R₀/ħ) = e^-λ',  λ' = √(2m/E) πU₀R₀/ħ
  e^-λ' is the transmission coefficient.
  To calculate the escape probability per second, we have to multiply T by the rate of the alpha particle hitting the barrier, which is approximately v/R₀.
  escape probability ≈  √(2m/E)/R₀ * e^-λ'  = λ = 1/τ.
  This is a reasonable order of magnitude approximation as long as the escape probability is very small.

Problem 2:

Let U(x) = ∞ for x < 0, U(x) = ½mω²x² for x > 0.  Use the WKB approximation to find the energy levels of a particle of mass m in this potential.  Compare the WKB energies with the exact energies for this potential.

Solution:

• Concepts:
  The WKB approximation
• Reasoning:
  We are instructed to use the WKB approximation. 
  For stationary bound states in a potential well with one vertical wall we want ∫₀^xmax pdx = (n - ¼)πħ, n = 1, 2, 3, ... .
• Details of the calculation:
  p = (2m(E - U(x))^1/2.
  For the given potential energy function
  ∫₀^xmax (2m(E - ½mω²x²)^1/2dx = (n - ¼)πħ.
  x_max = (2E/(mω²))^1/2.
  ∫₀^xmax (2m(E - ½mω²x²)^1/2dx = mω∫₀^xmax (2E/(mω²) - x²)^1/2dx
  = ½mω(2E/(mω²))(sin^-11 - sin^-10) = (E/ω)(π/2).
  (E/ω)(π/2) = (n - ¼)πħ,  E = (2n - ½)ħω.
  These are the exact energy levels for n = 1, 2, 3, ... .