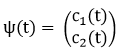 ,
, Problem 1:
Let A and B be two observables of a system with a two dimensional state space, and suppose measurements are made of A, B, and A again in quick succession. Show that the probability that the second measurement of A gives the same result as the first is independent of the initial state of the system.
Hint:
Let {|a1>,|a2> } be an othonormal eigenbasis of A
and let {|b1>,|ba> } be an othonormal eigenbasis of
B.
A|ai> = ai|ai>, B|bi> = bi|bi>.
|b1> = cos(θ)|a1> + sin(θ)eiφ|a2>, |b> =
-sin(θ)|a1>
+ cos(θ)eiφ|a2>
is the most general expansion of the |bi> in terms of the |ai>.
<b1|b2> = 0, <b1|b1> = <b2|b2>
= 1.
The initial state can be written as some linear combination of |a1>
and a2>.
|Ψ> = c1|a1> + c2|a2>.
Solution:
Branch 2:
Assume the first measurement yields a2. The probability for
this outcome is |c2|2.
What is the probability of measuring a2 again after a measurement of
B?
Pa2(b1) = sin2(θ) (system is now in state
|b1>), Pb1(a2) = sin2(θ),
Pa2(b1) Pb1(a2) = sin4(θ),
Pa2(b2) = cos2(θ) (system is now in state
|b2>), Pb2(a2) = cos2(θ),
Pa2(b2) Pb2(a2) = cos4(θ).
Probability of the first path + probability of the second path = sin4(θ)
+ cos4(θ).
Total probability for this branch: |c2|2(cos4(θ)
+ sin4(θ)).
Probability of obtaining the same result = (|c1|2 +
|c2|2)(cos4(θ) + sin4(θ))
= cos4(θ) + sin4(θ), independent of the initial
state.
Problem 2:
Find <x> and ∆x for the nth stationary state of a free particle in one dimension restricted to the interval 0 < x < a. Show that as n--> ∞ these become the classical values.
Solution:
The eigenfunctions of the infinite well (U(x) = 0, 0 < x < L,
U(x) = ∞ everywhere else) are
ψn(x) = (2/a)1/2sin(nπx/a)
with eigenvalues
En = n2π2ħ2/(2ma2).
<x> = ∫0a dx Ψ*(x) x Ψ*(x)
<x> = (2/a∫0a dx
x sin2(nπx/L) = a/2.
Δx = <(<x2> - <x>2)>1/2.
<x2> = (2/a∫0a dx
x2 sin2(nπx/L) = a2/3 - a2/(2n2π2).
Δx2 =
a2/3 - a2/4 - a2/(2n2π2)
=
a2/12 - a2/(2n2π2).
Δx2 -->
a2/12 as n --> ∞.
Classically the particle bounces back and forth. It spends the same
amount of time at each position.
Therefore xavg = a/2 for a large number of particles with arbitrary
initial positions.
x2rms = (1/a)∫0a dx (x - a/2)2 =(x3/3
- ax2/2 + a2x/4)|0a =
a2/12.
Problem 3:
A system makes transitions between eigenstates of H0
under the action of the time dependent Hamiltonian H0 + Wcosωt, W << H0.
Find an expression for the probability of transition from
||ψ1> to ||ψ2>,
where ||ψ1> and ||ψ2>
are eigenstates of H0 with eigenvalues E1 and E2.
Show that this probability is small unless E2 - E1 ≈ ħω.
[This shows that a charged particle in an oscillating electric field with angular
frequency w will exchange energy with the field only in
multiples of
E ≈ ħω.]
Solution:
Consider
a one-dimensional system, with momentum operator p and position operator q.
(a) Show that
[q,pn] = iħ n pn-1.
(b) Show that
[q,F(p)] = iħ ∂F/∂p, if
the function F(p) can be defined by a finite polynomial or convergent power series
in the operator p.
(c) Show that
[q,p2F(q)] = 2iħ pF(q) if F(q)
is some function of q only.
Solution:
Problem 5:
If
baryon number were not conserved in nature, the wave functions for neutrons
(n) and anti-neutrons (n) would not be stationary mass-energy
eigenfunctions.
Rather, the wave functions of such particles would be
oscillating, time-dependent superposition of neutron and anti-neutron
components, given by
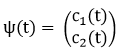 ,
,
Suppose
that such oscillations occur and the Hamiltonian of the system, neglecting
all degrees of freedom except for the one corresponding to the oscillations,
is
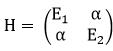 ,
,
where E1 = m + U1 and E2 = m +
U2 are energies for n and
n
individually, and α
is a real mixing amplitude.
In
an external magnetic field B, the potential energies are U1
= μ∙B
and U2
= -μ∙B
where μ
≈ μn = -μn.
Suppose
that at time t = 0 the initial state is that of a neutron.
(a) Calculate the time-dependent probability for observing an anti-neutron. Determine the period of oscillation.
Solution:
Let |n1> and |n2> denote the eigenstates of the
operator that distinguishes the neutron from the anti-neutron.
In this basis the matrix of H is
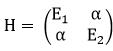 .
.
Let us rewrite H.
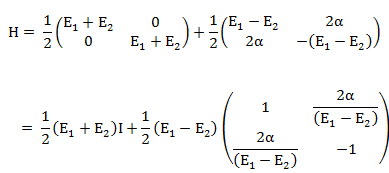
H = H1 + H2. H1 = ½(E1 + E2)I,
H2 = ½(E1 - E2)K.
Define tanθ = 2α/(E1 - E2), then
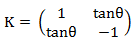 .
.
Since every vector is an eigenvector of I, the eigenvectors of K are the
eigenvectors of H.
The eigenvalues λ of K are found by solving det(K - λI) = 0.
λ2 = 1 + tan2θ, λ± = ±1/cosθ.
For the eigenvectors we have |ψ±> = c1|n1>+
c2|n2>.
For the eigenvector corresponding to λ+: (1 - 1/cosθ) c1
+ tanθ c2 = 0,
c2 = -c1(cosθ/sinθ)- 1/sinθ) = c1tan(θ/2).
|c1|2 + |c2|2 = 1 is satisfied
if c2 = sin(θ/2), c1 = cos(θ/2), |ψ+> =
cos(θ/2)|n1> + sin(θ/2)|n2>.
Similarly, for the eigenvector corresponding to λ- we find c1
= -c2tan(θ/2).
|c1|2 + |c2|2 = 1 is satisfied
if c1 = -sin(θ/2), c2 = cos(θ/2), |ψ-> =
-sin(θ/2)|n1> + cos(θ/2)|n2>.
|ψ+> and |ψ-> are the eigenvectors of H with eigenvalues E± = ½(E1 + E2) ± ½(E1 -
E2)/cosθ.
We have |n1> = cos(θ/2)|ψ+> - sin(θ/2)|ψ->, |n2>
= sin(θ/2)|ψ+> + cos(θ/2)|ψ->.
At t = 0 we have |ψ(0)> = |n1>.
|ψ(t)> = cos(θ/2)exp(-iE+t/ħ)|ψ+> - sin(θ/2)exp(-iE-t/ħ)|ψ->.
The probability of observing an antineutron at time t is Pn(t) = |<n2|ψ(t)>|2.
<n2|ψ(t)> = cos(θ/2) sin(θ/2)[exp(-iE+t/ħ) - exp(-iE-t/ħ)].
Pn(t) = ¼sin2θ[2 - exp(i(E+ - E-)t/ħ)
+ exp(i(E+ - E-)t/ħ)] = ½sin2θ [1 - cos((E+
- E-)t/ħ)].
Period of oscillation: 2π/T = (E+ - E-)/ħ, T =
h/(E+ - E-).
Let B = Bk, μ∙B = μzB.
Then E1 = m + μzB and E2 = m - μzB,
½(E1 + E2) = m, ½(E1 - E2) = μzB.
tanθ = α/μzB, 1/cos2θ = 1 + (α/μzB)2,
sin2θ = α2/(μz2B2 + α2).
E± = m ± (μz2B2 + α2)1/2,
E+ - E- = 2(μz2B2 + α2)1/2.
Pn(t) = ½[α2/(μz2B2 + α2)] [1 -
cos(2(μz2B2 + α2)1/2t/ħ)].
(b) The larger B, the shorter the period of the oscillations. However, The larger B, the smaller the amplitude of the oscillations.