Consider the one-dimensional potential step defined by U(x) = 0 , x < 0,  U(x) = U_0, x > 0.

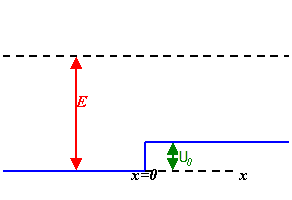
Suppose a wave incident from the left has energy E = 4U₀.  What is the probability that the wave will be reflected?

You are given a one dimensional potential barrier of height U which extends from x = 0 to x = a.  A particle of mass m and energy E < U is incident from the left.
(a)  Derive expressions for the coefficients of transmission T and reflection R for the barrier.
(b)  Show that T + R=1.

The one-dimensional square well shown in the figure rises to infinity at x = 0 and has range a and depth U₁.

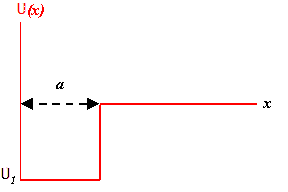
(a)  Derive the condition for a spinless particle of mass m to have two and only two bound states in the well.
(b)  Sketch the wave function of these two states inside and outside the well and give their analytic expressions.  These expressions may involve undetermined constants.

Problem 4:

Consider the scattering of a particle of mass m and total energy  E = ħ²k²/(2m) under the influence of a localized one-dimensional potential.
(a)  Let the potential be a delta function potential well, U(x) = -aU₀δ(x) with a > 0 and U₀ = ħ²k₀²/(2m).  What are the asymptotic boundary conditions at x = ∞ and the matching conditions at x = 0 for the wave function?
(b)  Define the transmission coefficient T and the reflection coefficient R and find the relationship between T and R.
(c)  How does the transmission coefficient depend on E?
(d)  Now the potential is replaced by a double delta function potential well.  The delta functions are a distance b apart, i.e. U(x) = -aU₀δ(x) - aU₀δ(x - b).  By inspecting the matching conditions without solving the algebra equation, explain intuitively the limiting behavior of the transmission coefficient T for E --> 0 and E --> ∞.