The Hamiltonian operator for a two state system is given by
H = a(|1><1|-|2><2|+|1><2|+|2><1|),
where a is a number with the dimensions of energy.  
(a)  Find the eigenvalues of H and the corresponding eigenkets |ψ₁> and |ψ₂> (as linear combinations of |1> and |2>).
(b)  A unitary transformation maps the {|1>, |2>} basis onto the {|ψ₁>, |ψ₂>} basis.  We have U|i> = |ψ_i>.  Write down the matrix of U and the matrix of U^† in the {|1>, |2>} basis.

Let P and Q be two linear operators and let [P,Q] = -iħ.  Find
(a)  [Q,P],
(b)  [Q,Pⁿ],
(c)  [P,Qⁿ] .

Suppose |i> and |j> are eigenkets of some Hermitian operator A.  Under what conditions can we conclude that |i> + |j> is also an eigenket?  Justify your answer.

Using the rules of bra-ket algebra, prove or evaluate the following:
(a)  tr(XY) = tr(YX), where X and Y are operators.
(b)  (XY)^† = Y^†X^†
(c)  exp(i f(A)) = ?, in ket-bra form, where A is a Hermitian operator whose eigenvalues are known.
(d)  ∑_a'ψ*_a'(r')ψ_a'(r''), where ψ_a'(r') = <r'|a'>.

Assume {|1>, |2>, |3>, ... , |n>} forms an orthonormal basis for the vector space V.  Let Ω_ij be the matrix elements of the Hermitian operator Ω in this basis.  Assume that the set {|1>, |2>, |3>, ... , |n>} is not an eigenbasis of Ω, but that the unitary transformation U|i> = |ω_i> changes this basis to the eigenbasis {|ω₁>, |ω₂>, |ω₃>, ... , |ω_n>} of Ω.  We have Ω|ω_i> = ω_i|ω_i>.  In this basis the matrix of Ω is diagonal.  Let U_ij denote the matrix elements of the unitary operator in the {|1>, |2>, |3>, ... , |n>} basis, U_ij = <i|U|j> = <i|ω_i>.  The matrix elements of Ω in the {|ω_i>} basis are the same as the matrix elements of U^†ΩU in the {|i>} basis.  The matrix of U^†ΩU in the {|i>} basis is diagonal, <i|U^†ΩU|j> = 0 if i ≠ j.
<i|U^†ΩU|j> = ∑_kl<i|U^†|k><k|Ω|l><l|U|j> =  ∑_klU^†_ikΩ_klU_lj.
We can therefore diagonalize the matrix Ω by multiplying it from the left by U^† and from the right by U.
Consider the matrix 
 
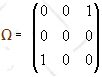
 in the {|i>} basis.

(a)  Is this matrix Hermitian?
(b)  Find its eigenvalues ω_i and eigenvectors |ω_i>.
(c)  Find the matrix of U in the {|i>} basis.
(d)  Find the matrix of U^† in the {|i>} basis. (U changes {|i>} into {|ω_i>}.)
(e)  Verify that UU^† = U^†U = I.
(f)  Verify that the matrix U^†ΩU in the {|i>} basis is diagonal.