Let A and B be two observables of a system with a two dimensional state space, and suppose measurements are made of A, B, and A again in quick succession.  Show that the probability that the second measurement of A gives the same result as the first is independent of the initial state of the system.

Problem 2:

Find <x> and ∆x for the nth stationary state of a free particle in one dimension restricted to the interval 0 < x < a.  Show that as n--> ∞ these become the classical values.

Problem 3:

A system makes transitions between eigenstates of H₀ under the action of the time dependent Hamiltonian H₀ + Wcosωt, W << H₀. 
Find an expression for the probability of transition from ||ψ₁> to ||ψ₂>, where ||ψ₁> and ||ψ₂> are eigenstates of H₀ with eigenvalues E₁ and E₂. 
Show that this probability is small unless E₂ - E₁ ≈ ħω.
[This shows that a charged particle in an oscillating electric field with angular frequency w will exchange energy with the field only in multiples of E ≈ ħω.]

Consider a one-dimensional system, with momentum operator p and position operator q.
(a) Show that [q,pⁿ] = iħ n p^n-1.
(b) Show that [q,F(p)] = iħ ∂F/∂p, if the function F(p) can be defined by a finite polynomial or convergent power series in the operator p.
(c) Show that [q,p²F(q)] = 2iħ pF(q) if F(q) is some function of q only.

Problem 5:

If baryon number were not conserved in nature, the wave functions for neutrons (n) and anti-neutrons (n) would not be stationary mass-energy eigenfunctions.
Rather, the wave functions of such particles would be oscillating, time-dependent superposition of neutron and anti-neutron components, given by

,

where n = 1,  n = 2.

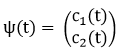Suppose that such oscillations occur and the Hamiltonian of the system, neglecting all degrees of freedom except for the one corresponding to the oscillations, is

,

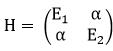where  E₁ = m + U₁  and  E₂ = m + U₂  are energies for n and n individually, and α is a real mixing amplitude.
In an external magnetic field B, the potential energies are U₁ = μ∙B and U₂ = -μ∙B where μ ≈ μ_n = -μ_n.
Suppose that at time t = 0 the initial state is that of a neutron.
(a)  Calculate the time-dependent probability for observing an anti-neutron. Determine the period of oscillation.
(b)  Describe the effect of increasing the external magnetic field.