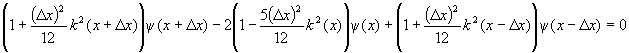4th order Taylor series expansion:
ψ(x + ∆x) = ψ(x) + ∆x*∂ψ(x)/∂x + [(∆x)²/2]*∂²ψ(x)/∂x² + [(∆x)³/3!]*∂³ψ(x)/∂x³ + [(∆x)⁴/4!]*∂⁴ψ(x)/∂x⁴ + ... .
ψ(x - ∆x) = ψ(x) - ∆x*∂ψ(x)/∂x + [(∆x)²/2]*∂²ψ(x)/∂x² + [(∆x)³/3!]*∂³ψ(x)/∂x³ + [(∆x)⁴/4!]*∂⁴ψ(x)/∂x⁴ + ... .
Combining the two equations above yields
[ψ(x + ∆x) + ψ(x - ∆x) - 2ψ(x)]/(∆x)²
= ∂²ψ(x)/∂x² + [(∆x)⁴/12]*∂⁴ψ(x)/∂x⁴  + O((∆x)⁴ ).  (equation 1)
Here O((∆x)⁴) denotes terms of higher than fourth order in ∆x.

From the Schroedinger equation,
∂²ψ(x)/∂x² - k(x)²ψ(x) = 0,
we obtain
∂⁴ψ(x)/∂x⁴ = ∂²/∂x²(k²(x)ψ(x))
= [k²(x + ∆x)ψ(x + ∆x)  +  k²(x - ∆x)ψ(x - ∆x)  - 2k(x)²ψ(x)]/(∆x)²,
or
(∆x)²∂⁴ψ(x)/∂x⁴ = k²(x + ∆x)ψ(x + ∆x)  +  k²(x - ∆x)ψ(x - ∆x)  - 2k(x)²ψ(x).
 

Inserting this expression into equation (1) and neglecting terms of higher than fourth order in ∆x we obtain
.
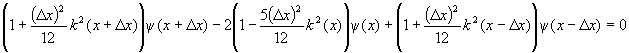or, for solving on a grid,

.
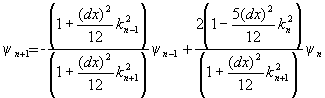