

Consider a two-particle system, consisting of a neutron and a proton. In addition to the dominant Wigner component (central, non-exchange potential), of the nucleon-nucleon interaction, there are exchange forces, which play important roles. One of these is the Bartlett exchange component, which may be represented by a potential VB=-PBV(r), V(r)>0, where PB is an operator which exchanges the spins of the two nucleons and V(r) is a central potential.
(a) Write down the possible intrinsic spin wavefunctions for the n-p system and the Schroedinger equation for two nucleons subject to the above potential. Use these to demonstrate that the presence of the Bartlett force provides a partial explanation for the spin character of the ground state of the deuteron.
(b) How would the above be modified if the two nucleons each had the same t3 component of nuclear isospin. Use this to give a partial explanation for the lack of a bound state for the 2-proton system.
Use first-order perturbation theory to estimate the energy difference between the singlet and triplet states of the (1s2s) configuration in helium. The 2s single particle state in helium is
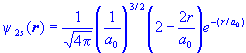 .
.
Consider a coupled pair of one-dimensional, distinguishable, simple harmonic oscillators with equal masses, equal individual potentials V(x1)=½Cx12, V(x2)=½Cx22, C>0, and a coupling potential Vc(x1,x2)=½k(x2-x1)2, k>0.
(a) Separate the Hamiltonian in center of mass and relative
variables R=½(x1+x2) and r=(x2-x1).
(b) Show that the total eigenfunction can be written as a product of two functions
and determine the energy eigenvalues of the coupled system of distinguishable particles.
(c) Now assume that the particles are indistinguishable so that they are either
Bosons or Fermions. Using the symmetry properties of the product functions determined in
part (b), determine which of the energy levels found in part (b) are associated with each
type of particle.
(d) Show that for Fermions, the probability of finding the two particles at r=0 is
zero.
(Note: In this problem, you may use your knowledge of the wavefunctions and eigenvalues of the simple harmonic oscillator without derivation or proof.)